【每日一题1203】环形面积

兴趣爱好交流 每日一题
1

已知一个长度是a的线段，以及由它中点处与内圆环绕相切所形成的体环图形。
请编写一个函数，求出图中灰色部分的圆环面积，结果保留2位小数。

备注：

  1. 线段长度a 是大于1的整数。
  2. 圆周率请使用内置常量，例如Python中使用math.pi。

image

题目难度：简单
题目来源：Codewars：Area of an annulus

def solution(a: int) -> float:
    # your code

assert solution(7) == 38.48
assert solution(13) == 132.73
2
3
4 
import math


def solution(a: int) -> float:
    # your code
    area = (a / 2) ** 2 * math.pi
    return round(area, 2)


assert solution(7) == 38.48
assert solution(13) == 132.73
5 
import math
# 圆环面积 = PI * R ** 2 - PI * r ** 2
#                 = (R ** 2 - r**2) * PI 
# 根据勾股定理得  : a / 2 ** 2 * PI
def solution(a: int) -> float:
    
    return float('%.2f' % ((a / 2) ** 2 * math.pi))


assert solution(7) == 38.48
assert solution(13) == 132.73
6

image

8 
def solution(a: int) -> float:
    return round((a / 2) ** 2 * math.pi, 2)


assert solution(7) == 38.48
assert solution(13) == 132.73
9

def solution(a: int) → float:
i = float(format((1/4)aa*pi, ‘.2f’))
return i

10 
def solution(a: int) -> float:
    # y*y + a/2 * a/2 = x * x
    #wai = math.pi * (y*y + a/2 * a/2)
    #nei = math.pi * y*y
    return round(math.pi * a/2 * a/2,2)
11

Python 参考题解：

def solution(a: int) -> float:
    import math
    
    return round(math.pi * (a / 2) ** 2, 2)

assert solution(7) == 38.48
assert solution(13) == 132.73

思路：这题主要考察几何知识。先作出两条辅助线段：1条是从圆心连接切点的绿色线段；1条是从圆心连接线段a的断点的蓝色线段。

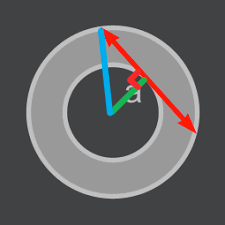
image

根据几何知识我们知道，绿色和线段a是垂直的。
灰色环形的面积=π*蓝色线段长2 - π*绿色线段长2，根据勾股定理，即灰色环形面积= π*(a/2)2。

12 
import math
from decimal import Decimal


def solution(a: int) -> float:
    result = math.pi * (a / 2) ** 2
    return float(Decimal(result).quantize(Decimal("0.00")))


assert solution(7) == 38.48
assert solution(13) == 132.73