一、函数
- 函数是组织好的,可重复使用的,用来实现单一或相关联功能的代码段
- 函数能提高应用模块性和代码的重复利用率
函数定义
- 实现了某一功能,可被重复使用的代码段
- 参数的意义是从外面与函数里面沟通,返回值的意义是里面与外面沟通
-
def:函数定义关键词 -
function_name:函数名称 -
():参数列表放置的位置,可以为空 -
parameter_list:可选,指定向函数中传递的参数 -
comments:可选,指定函数体 - 定义一个函数:
def func(parameters):
#函数注释,功能说明
代码
return value
return 结束函数执行
def show():
print("循环前输出内容")
for i in range(10):
print(i)
if i == 2:
return
print("循环后输出内容")
print("函数调用前输出内容")
show()
print("函数调用后输出内容")

函数只能返回一个值
一个函数只能返回一个结果值,当需要返回多个值时,需要进行包装处理。
def getString():
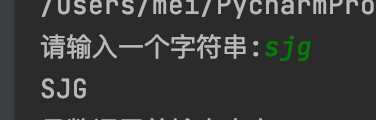
s = input("请输入一个字符串:")
return s
result = getString()
print(result.upper())
def getTwoNum():
a = int(input("请输入第一个数字:"))
b = int(input("请输入第二个数字:"))
return a, b
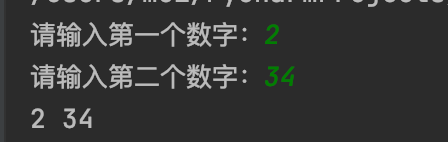
m, n = getTwoNum()
print(m, n)
通过代码发现,函数执行结果和前面介绍的理论并不符合,但实际上,该函数返回的依然是一个值,只是Python在执行时,自动做了组包和解包操作。
def getTwoNum():
a = int(input("请输入第一个数字:"))
b = int(input("请输入第二个数字:"))
return a, b
result = getTwoNum()
print(result)
print(type(result))
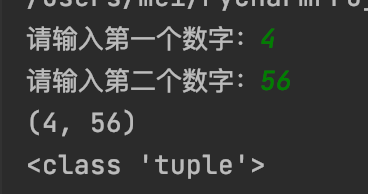
通过代码执行结果发现,使用一个变量,也可以接收返回的两个数据,并且变成了一个元组。这就是组包操作。
组包与解包
# 组包
nums = 1,2,3,4,5
print(nums)
print(type(nums))
# 解包
a,b,c,d,e = nums
print(a,b,c,d,e)
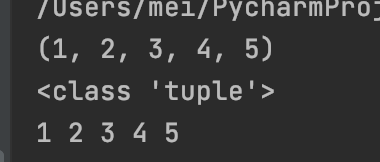
通过代码可以发现,当将多个值,同时赋给一个变量时,Python会进行自动组包操作,将所有的数字组合成一个元组,再将元组赋值给变量。 当使用一个元组为多个变量进行赋值时,Python会将元组中的元素值,依次赋值给变量,这称为解包操作。
由此可以看出,上一小节中的函数依然返回的是一个结果值,结果值的类型是一个元组。
多个return语句
在一个函数中,允许有多个return语句,可以实现在不同的条件下,返回不同的值,但同一时刻,只能有一个return语句被执行。
def multiReturn():
return 1
return 2
return 3
return 4
return 5
print(multiReturn())
print(multiReturn())
print(multiReturn())
print(multiReturn())
print(multiReturn())
通过代码发现,虽然函数提供了5条return语句,并返回了不同的结果值,在调用时,也调用了五次,但实际,5次的调用结果都是相同的,都为1
参数传递
- 主调函数:主动调用其它函数执行的称为主调函数。
- 被调函数:被动调用执行的函数称为被调函数。
- 实际参数:在调用函数的时候,函数名称后面括号中的数据即为实际参数,简称实参,通俗讲就是实际值。
- 形式参数:在定义函数的时候,函数名称后面括号中的变量即为形式参数,称称形参,通俗讲就是一个记号。
- 无返回;有返回、无参数;有参数;有多个参数
- 函数多种形参类型—通用性(标志位法)。必填、缺省、可变args、关键字kwargs
# name, age, gender 为形参
def info(name, age, gender):
print(f"我叫{name}, 年龄{age}岁,性别{gender}")
# 调用时的数据为实参
info("Tom", 22, "男")
info("Rose", 23, "女")
# a,b,c为形式参数
def func_with_params(a, b, c):
'''
这是一个携带参数和注释的函数
:param a:
:param b:
:param c:
:return:
'''
print(f'传入的参数为:a={a},b={b},c={c}')
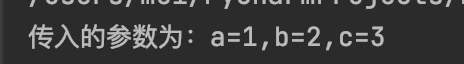
位置参数
位置参数也称为必备参数,必须按照正确的顺序传到函数中,即调用时的数量和位置必须 和定义时是一样的。
- 数量必须与定义时一致,在调用函数时,指定的实际参数的数量必须与形式参数的数量一致,否则将抛出 TypeError 异常,提示缺少必要的位置参数(missing x required positional argument)。
- 位置必须与定义时一致,在调用函数时,指定的实际参数的位置必须与形式参数的位置一致,否则将抛出 TypeError 异常或者结果与预期不符的情况,例如入参的位置 1 需要一个 int 类型参数,而入参 2 位置需要一个 str 类型的参数,如果传递的位置不正确,那么 str 类型数据传递进去之后会报类型错误的异常;位置参数是会按照顺序进行参数的替换的。
# 位置参数
def person(name, age, nationlity='中国'):
print(f"姓名为:{name}")
print(f'国籍为{nationlity}')
if age >= 18 :
print(f"{name}已成年")
else:
print(f"{name}未成年")
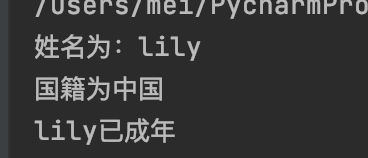
关键字参数
关键字参数是指使用形式参数的名字来确定输入的参数值,通过该方式指定实际参数时,不再需要与形式参数的位置完全一致,只要将参数名写正确即可,这样可以避免用户需要牢记参数位置的麻烦,使得函数的调用和参数传递更加灵活方便。
默认值参数
在定义函数时,形参可以定义变量一样进行赋值,这个值就是默认该参数的默认值,调用函数时,如果指定了该参数的数据,则使用指定的数据,如果没有指定该参数的数据,则使用默认值的数据。
# 错误示范,默认值为空列表
# 默认值一定要用不可变对像,否则的话默认值可能会随着调用发生变化
def wrong_demo2(a, b, c=[]):
c.append(a)
c.append(b)
print(a, b, c)
def hello_func(greeting, name='linda'): # greeting位置参数,name关键字参数,后面是默认值
return '{} {} 你好'.format(greeting, name)
print(hello_func('hi'))
print(hello_func('hi', 'emily'))
def student_info(*args, **kwargs): # *args 用来将参数打包成元组给函数体调用,**kwargs 打包关键字参数成字典给函数体调用
print(args)
print(kwargs)
print(*args) # 按元组类型解包
print(**kwargs) # 按字典类型解包
courses = ['python', 'java']
info = {'name': 'linda', 'age': 18}
student_info(courses, info)
def foo(x, *args, a=4, **kwargs): # 使用默认参数时,注意默认参数的位置在args后面的kwargs
print(x)
print(a)
print(args)
print(kwargs)
foo(1, (5, 6, 7, 8), {'y': 2, 'z': 3})
foo(1, *(5, 6, 7, 8), **{'y': 2, 'z': 3})
# 注意点:参数arg、*args、**kwargs三个参数的位置必须是一定的。必须是(arg,*args,**kwargs)这个顺序,否则程序会报错
运行结果:
hi linda 你好
hi emily 你好
(['python', 'java'], {'name': 'linda', 'age': 18}) # print(args)
{} #print(kwargs)
['python', 'java'] # print(args)
{'name': 'linda', 'age': 18} #print(kwargs)
1
4
((5, 6, 7, 8), {'y': 2, 'z': 3})
{}
1
4
(5, 6, 7, 8)
{'y': 2, 'z': 3}
可变参数
- Python使用
*args参数做为形参,接收不确定个数的位置参数。 -
*args将接收到的任意多个实际参数放到一个元组中。
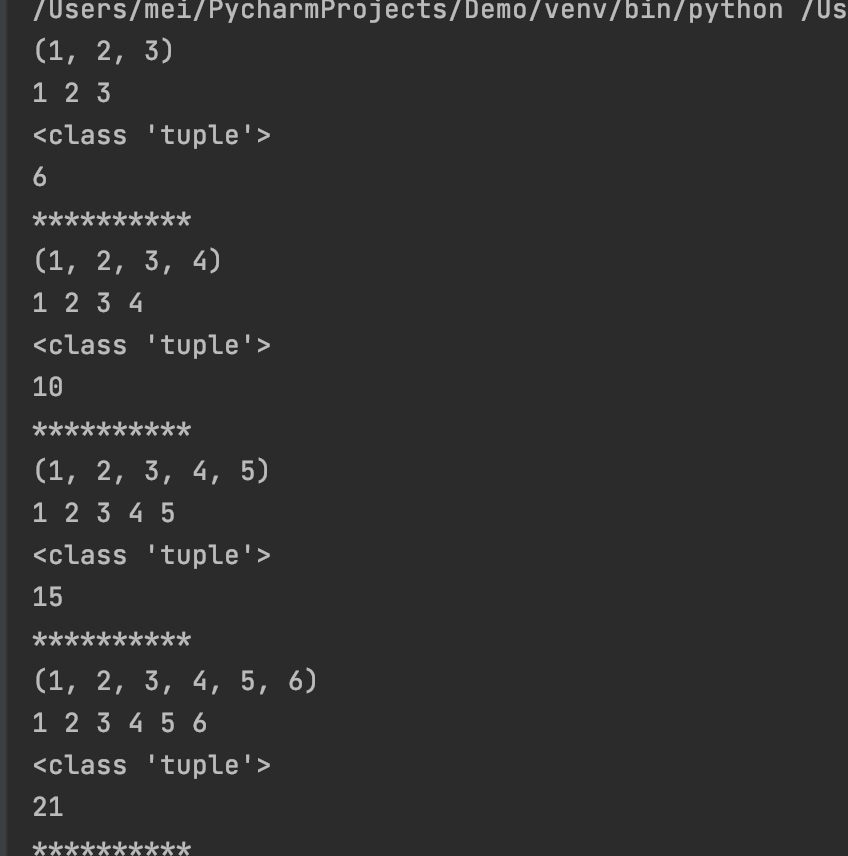
# 不确定个数数字求和
def my_sum(*args):
print(args)
print(*args)
print(type(args))
s = 0
for i in args:
s += i
print(s)
print("*" * 10)
my_sum(1,2,3)
my_sum(1,2,3,4)
my_sum(1,2,3,4,5)
my_sum(1,2,3,4,5,6)
可变关键字参数
- Python使用
**kwargs参数做为形参,接收不确定个数的关键字参数。 -
**kwargs将接收到的任意多个实际参数放到一个字典中。
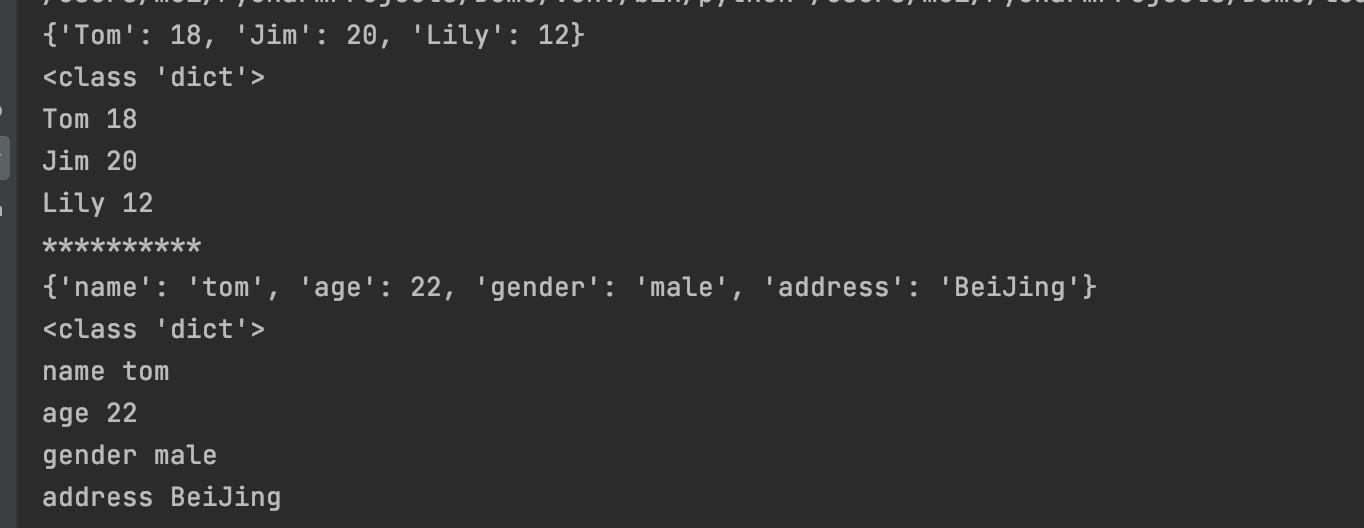
# 定义可变关键字参数
def print_info(**kwargs):
print(kwargs)
print(type(kwargs))
for k,v in kwargs.items():
print(k, v)
print("*" * 10)
print_info(Tom=18, Jim=20, Lily=12)
print_info(name="tom",age=22,gender="male",address="BeiJing")
混合参数
当定义函数时,参数列表中出现了多种类型的参数,定义时需要注意参数的定义顺序,如果顺序使用不正确,在调用函数时,可能会报错。
正确顺序的定义为:位置参数,可变位置参数,默认值参数,可变关键字参数
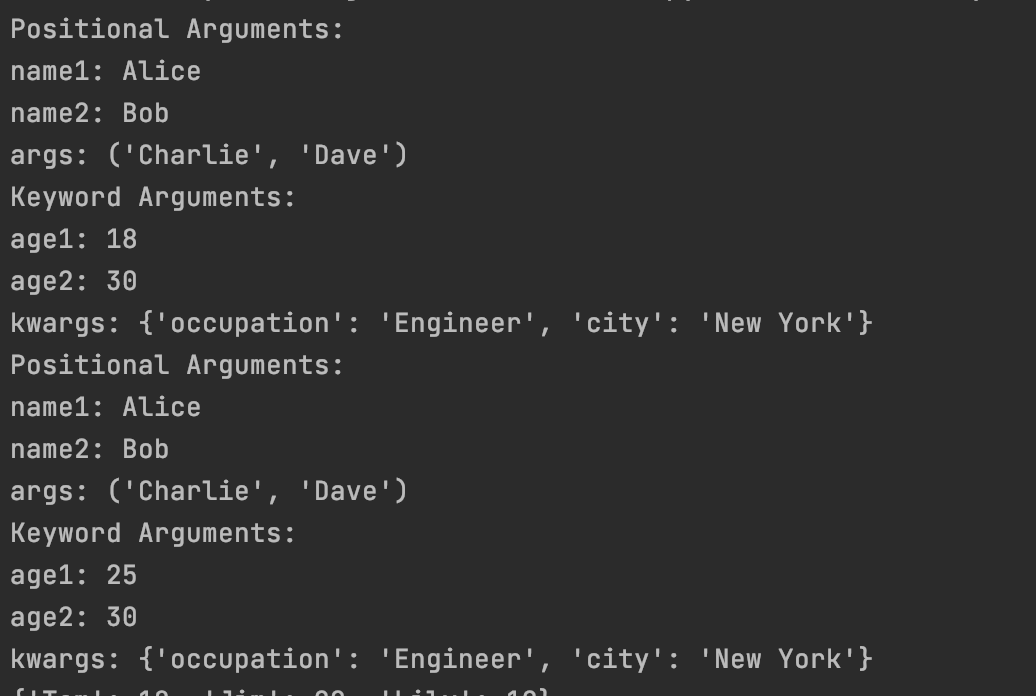
def info(name1, name2, *args, age1=18, age2=21, **kwargs):
print("Positional Arguments:")
print("name1:", name1)
print("name2:", name2)
print("args:", args)
print("Keyword Arguments:")
print("age1:", age1)
print("age2:", age2)
print("kwargs:", kwargs)
info("Alice", "Bob", "Charlie", "Dave", age2=30, occupation="Engineer", city="New York")
info("Alice", "Bob", "Charlie", "Dave", age1=25, age2=30, occupation="Engineer", city="New York")
一般函数在不确定参数的情况下,会将上面的形式简化定义,用来接收任意数量的参数。
def funcname(*args, **kwargs):
pass
在此定义形式中,使用 *args 接收所有的位置参数,使用 **kwargs 接收所有的关键字参数。
需要注意的是,传递参数时,需要先传递完所有的位置参数后,才能传递关键字参数。
二、变量作用域
在一个 Python 程序中,直接访问一个变量,会从内到外依次访问所有的作用域直到找到,否则会报未定义的错误。
Python 中,程序的变量并不是在哪个位置都可以访问的,访问权限决定于这个变量是在哪里赋值的。
变量的作用域决定了在哪一部分程序可以访问哪个特定的变量名称。Python 的作用域一共有4种,分别是:
有四种作用域:
-
L(Local):最内层,包含局部变量,比如一个函数/方法内部。 -
E(Enclosing):包含了非局部(non-local)也非全局(non-global)的变量,一般在闭包中出现。 -
G(Global):当前脚本的最外层,比如当前模块的全局变量。 -
B(Built-in): 包含了内建的变量/关键字等,最后被搜索。
查找规则顺序: L –> E –> G –> B。
在局部找不到,便会去局部外的局部找(例如闭包),再找不到就会去全局找,再者去内置中找。
根据作用域的不同,变量可分为局部变量和全局全量。
局部变量
局部变量是指在函数内部定义并使用的变量,它只在函数内部有效,即函数内部的名字只在函数运行时才会创建,在函数运行之前或者运行完毕之后,所有的名字就都不存在了。 所以,如果在函数外部使用函数内部定义的变量,就会抛出 NameError 异常。
def show():
# 局部变量
a = 10
print(a)
# 在函数外无法访问局部变量a
# print(a)
# 只能通过调用函数使用局部变量
show()
# 函数外无法访问局部变量a
# print(a)
输出:10
定义在函数内部的局部变量,只在函数内部可以被访问。局部变量在函数被调用时被创建,在函数执行结束后被销毁。
全局变量
定义在函数外之外的变量为全局变量,全局变量可以在当前程序文件的任何位置进行访问 。
# 全局变量定义
m = 20
def show1():
# 使用全局变量
print("show1:", m)
def show2():
# 使用全局变量
print("show2:", m)
# 使用全局变量
print(m) #20
show1() # show1:20
show2() # show2:20
# 使用全局变量
print(m) #20

当全局变量和局部变量同名时,根据作用域的查找规则顺序,内部变量会屏蔽全局变量。
# 全局变量定义
m = 10
def show():
# 局部变量与全局变量同名
m = "ABC"
# 使用局部变量
print("show:", m)
# 使用全局变量
print(m)
show()
# 使用全局变量
print(m)

从上面的代码中可以看出,如果想在函数内部修改全局变量时,会被解释成同名变量屏蔽,此时,需要使用 global 关键字
# 全局变量定义
m = 10
def show():
# 声明此变量是函数外定义的全局变量
global m
# 修改全局变量的值
m = "ABC"
# 使用全局变量
print("show:", m)
# 使用全局变量
print(m)
show()
# 使用全局变量
print(m)

与局部变量对应,全局变量为能够作用于函数内外的变量。全局变量主要有两种情况。
情况一:如果一个变量在函数体外定义,那么不仅在函数外可以访问到,在函数内也可以访问到。在函数体以外定义的变量是全局变量。
改造一下前面局部变量的例子
msg = "学习测试开发来霍格沃兹测试学社" # 创建一个局部变量并赋值
def var_demo():
print("函数体内全局变量 msg 的值为", msg) # 输出局部变量 msg 的值
var_demo() # 调用函数
print("函数体外全局变量 msg 的值为", msg) # 在函数体外输出局部变量的值
上面的例子中,在 var_demo 函数中创建之前就定义了一个 msg 变量,在函数之外属于全局变量;在函数的内部直接使用该变量是正常的,能正常输出赋予的值;在函数体之外进行变量值的输出的时候,也会正常的输出,不会抛出 NameError 异常。注意,当局部变量与全局变量重名时,对函数体内的变量进行赋值后,操作的是局部变量,不影响函数体外的变量。
情况二:如果一个变量在函数体内定义,并且使用 global 关键字修饰后,该变量也就变为全局变量。在函数体外可以访问该变量,并且在函数体内还可以对其进行修改。
改造一下全局变量的例子
msg = "学习测试开发来霍格沃兹测试学社" # 创建一个局部变量并赋值
print("函数体外全局变量 msg 的值为", msg) # 在函数体外输出局部变量的值
def var_demo():
msg = "霍格沃兹测试学社值得信赖" # 创建一个局部变量并赋值
print("函数体内变量 msg 的值为", msg) # 输出局部变量 msg 的值
var_demo() # 调用函数
print("函数体外全局变量 msg 的值为", msg) # 在函数体外输出局部变量的值
改造成为当前的模式之后实际上局部变量与全局变量重名时,对函数体内的变量进行赋值后,操作的是局部变量,不影响函数体外的变量。
如果想要实现函数内容修改全局变量的值就需要借助 global 来实现
进一步改动全局变量的例子
msg = "学习测试开发来霍格沃兹测试学社" # 创建一个局部变量并赋值
print("函数体外全局变量 msg 的值为", msg) # 在函数体外输出局部变量的值
def var_demo():
global msg
msg = "霍格沃兹测试学社值得信赖" # 此时已经申明了 msg 为全局变量
print("函数体内变量 msg 的值为", msg) # 输出局部变量 msg 的值
var_demo() # 调用函数
print("函数体外全局变量 msg 的值为", msg) # 在函数体外输出局部变量的值
全局变量和局部变量的优缺点
全局变量的优点:
- 全局变量在整个程序中都可访问,方便在不同的函数或模块之间共享数据。
- 全局变量可以保存程序运行期间的状态,比如计数器或状态标志。
全局变量的缺点:
- 全局变量的作用范围很大,容易被误修改,导致程序出现错误。
- 在多个函数中使用同名的全局变量时,很容易出现混淆和命名冲突的问题。
- 全局变量的使用不宜过多,因为它们会占用内存资源。如果程序中有太多的全局变量,会增加维护和调试的难度。
局部变量的优点:
- 局部变量的作用范围限于所在的函数或代码块中,不会对其他函数或模块造成影响。这样可以防止变量的误修改或命名冲突。
- 局部变量仅在需要时才会被创建和销毁,节省了内存资源。
局部变量的缺点:
- 局部变量的作用范围有限,不能在其定义范围外直接访问。如果需要在多个函数之间共享数据,就不能使用局部变量,需要采用其他的方式来传递数据。
- 当函数中定义了较多的局部变量时,可能会使代码显得冗长和难以阅读,增加了编写和维护的复杂性。
在编写程序时,应根据具体的需求来选择使用全局变量还是局部变量。如果需要在多个函数中共享数据,可以选择使用全局变量;如果只在某个函数内部使用的变量,可以选择使用局部变量。同时,需要注意合理命名变量,以避免命名冲突和混淆。
作业
编写一个Python程序,输入一个正整数,判断这个数是否为素数(质数)。素数是指只能被1和它本身整除的正整数。
import math
num = int(input("请输入一个正整数:\n"))
def sushu(n):
"""
编写一个Python程序,输入一个正整数,判断这个数是否为素数(质数)。素数是指只能被1和它本身整除的正整数。
:return:
"""
if n <= 1:
return False
for i in range(2, int(math.sqrt(n))+1):
if n % i == 0:
return False
return True
if sushu(num):
print(f"{num}是素数")
else:
print(f"{num}不是素数")

三、匿名函数:
在 Python 中使用 lambda 表达式创建匿名函数。
- Lambda 函数可用于任何需要函数对象的地方。
- 在语法上,匿名函数只能是单个表达式。
- 在语义上,它只是常规函数定义的语法糖。
- lambda 表达式中不能使用 if,for,while, return等语句, 但可以使用三目运算符
匿名函数格式
result = lambda [arg1 [, arg2, .... , argn]]: expression
- result:用于保存 lambda 表达式的引用
- [arg1 [, arg2, … , argn]]:可选,指定要传递的参数列表,多个参数间使用英文的逗号
,进行分隔。 - expression:必选,指定一个实现具体功能的表达式。如果有参数,那么在该表达式中将应用这些参数。
# 匿名函数:不声明函数名
add = lambda x, y: x+y
add1 = lambda *args: sum(args)
print(add(34, 87))
print(add1(1, 56, 35))
func = lambda x: x**2 if x > 3 else x**3
print(func(3))
输出:
121
92
27
使用场景
- 需要一个函数,但是又不想费神去命名这个函数
- 通常在这个函数只使用一次的场景下
- 可以指定短小的回调函数
比如,在学习列表时的sort()排序方法,如果是简单的基本数据类型的数据,可以直接进行排序,但如果是复杂结构的数据,需要根据自定义的规则进行排序,此时就可以使用lambda。
# 待排序的数据
students = [
{'name': 'Alice', 'id': '1001', 'class': 'Class1'},
{'name': 'Eve', 'id': '1005', 'class': 'Class2'},
{'name': 'Charlie', 'id': '1003', 'class': 'Class1'},
{'name': 'David', 'id': '1004', 'class': 'Class2'},
{'name': 'Bob', 'id': '1002', 'class': 'Class1'},
{'name': 'Frank', 'id': '1006', 'class': 'Class2'}
]
# TypeError: '<' not supported between instances of 'dict' and 'dict'
# students.sort()
# 以名字排序
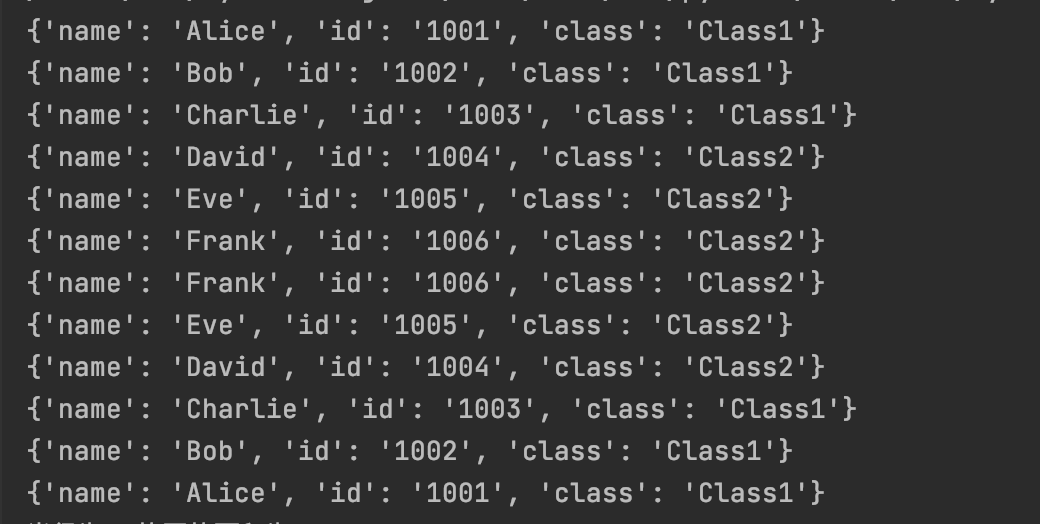
students.sort(key=lambda stu: stu["name"])
for s in students:
print(s)
# 以ID降序排序
students.sort(key=lambda stu: stu["id"],reverse=True)
for s in students:
print(s)
Sorted函数实现原理
students = [
{'name': 'Alice', 'id': '1001', 'class': 'Class1'},
{'name': 'Eve', 'id': '1005', 'class': 'Class2'},
{'name': 'Charlie', 'id': '1003', 'class': 'Class1'},
{'name': 'David', 'id': '1004', 'class': 'Class2'},
{'name': 'Bob', 'id': '1002', 'class': 'Class1'},
{'name': 'Frank', 'id': '1006', 'class': 'Class2'}
]
def mySorted(obj, key=None, reverse=False):
newStus = []
for s in students:
for n in newStus:
if key:
if(key(s) < key(n)):
idx = newStus.index(n)
newStus.insert(idx, s)
break
else:
if (s < n):
idx = newStus.index(n)
newStus.insert(idx, s)
break
else:
newStus.append(s)
return newStus if reverse else newStus[::-1]
# students = mySorted(students, key=lambda s: s["name"])
# students.sort(key=lambda s: s["name"])
students = [1,4,2,6,7,8,4,3,3]
students = mySorted(students, reverse=True)
print(students)
for s in students:
print(s)

四、递归算法
递归的基本原则
递归函数通常遵循以下原则:
- 定义基本情况:确定一个或多个输入的特殊情况,当满足这些条件时,递归函数将直接返回结果而不再调用自身。
- 减小问题规模:通过调用自身来解决一个规模更小的问题,这样每次递归调用都在问题规模上取得了进展。也就是需要一个已定义好的规则来使其它非基本的情况转化为基本情况。
- 终止条件:递归函数必须包含能够导致函数不再递归调用的条件,以避免无限递归。
递归使用举例-阶乘
数学中有一个比较经典的递归算式就是求阶乘
一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。 对阶乘的定义进行分析:
- 首先定义 f(n) 为阶乘函数。它的结果就是阶乘计算之后的值。
- 从定义中能得到基本情况为: f(0) = 1, f(1) = 1
- 其它情况:
f(2) = 2*1 = 2*f(1),f(3) = 3*2*1 = 3*f(2)即f(n) = f(n-1) * n
接下来把分析的结果转换成 Python 代码
def f(n):
"""
实现计算 n 的阶乘
return:n 阶乘计算之后的值
"""
if n == 0 or n == 1:
# 对应基本情况
return 1
return f(n - 1) * n # 对应递归情况
大多数情况下的递归操作都可以使用循环所替代。
在使用递归时,要注意避免陷入无限调用而产生的内存溢出。
作业
阶乘
def f(n):
if n ==0 or n == 1:
return 1
else:
return f(n-1) * n
斐波那契数列
def feibo(n):
"""
编写一个Python程序,使用递归算法,
生成并输出斐波那契数列的前n项,
其中n是用户指定的正整数。
斐波那契数列,又称黄金分割数列,
指的是:1、1、2、3、5、8、13、21、34....从第三个数开始,
每个数字都是前两个数字之和。
:return:
"""
if n < 3:
return 1
else:
return feibo(n-2) + feibo(n-1)