算法性能评估-python
规模:数据的大小对算法至关重要
测试环境:
运行环境:环境的快慢对算法至关重要
算法的运行时间与数据规模成正比
空间复杂度是存储空间与数据规模之间的增长关系
概论
- 时间复杂度
- 空间复杂度
时间复杂度
- 规模: 不同量级有不同的速度,比如水 vs 水杯: 水
- 测试环境: 在不同测试环境,速度也不同,比如手机 vs 电脑: 电脑的速度更快
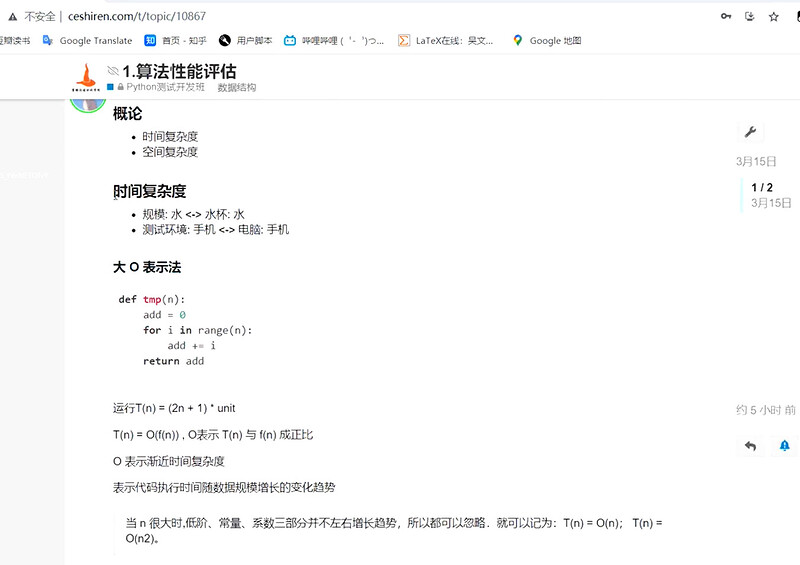
大 O 表示法
- 运行时间:T(n) = (2n + 1) * unit
- T(n) = O(f(n)) , O表示 T(n) 与 f(n) 成正比
- O 表示渐近时间复杂度
- 表示代码执行时间随数据规模增长的变化趋势
- 当 n 很大时,低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略.就可以记为:T(n) = O(n); T(n) = O(n2)。
def tmp(n):
add = 0
for i in range(n):
add += i
return add
只关注循环次数多的代码
def tmp(n):
add = 0
for i in range(n):
add += i
return add
O(n)
选大量级
def tmp(n):
for i in range(999):
print(123)
for i in range(n):
print(1)
for i in range(n):
for j in range(n):
print(2)
O(n2)
嵌套循环要乘积
def tmp(n):
for i in range(n):
a(i)
def a(n):
for i in range(n):
print('c')
O(n2)
常见复杂度分析
- 非多项式量级(过于低效) : O(2n) 和 O(n!)
- 多项式量级:O(1), O(logn), O(n), O(nlogn), O(nk)
空间复杂度
- 渐进时间复杂度:表示算法的执行时间与数据规模之间的增长关系。
- 渐进空间复杂度:表示算法的存储空间与数据规模之间的增长关系。
def tmp(n):
a = [1]*n
for i in a:
print(i)
空间复杂度是: O(n)