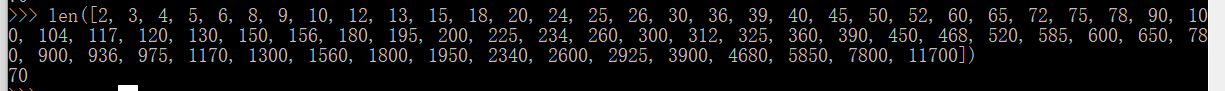【每日一题20220915】通过素数分解遵循数字的路径

兴趣爱好交流 每日一题
1

:technologist:您将获得一个数字的素数作为数组。例如：[2,2,2,3,3,5,5,13]

您需要找到该素数分解所属的数字 n。这将是：

n = 2³*3²*5²*13 = 23400

然后，生成这个数的除数。

您的函数get_num() or getNum() 将接收一个具有潜在无序素数因子的数组，并应输出：在索引 0 处具有找到的整数 n 的数组，在索引 1 处的总除数（素数和复合数）的数量，然后是最小因子（索引 2），和最大的一个（最后一个元素）

我们将看到上面给出的示例，唯一的区别是素因子数组是无序的。

该数字 (23400) 的除数列表是：

2, 3, 4, 5, 6, 8, 9, 10, 12, 13, 15, 18, 20, 24, 25, 26, 30, 36, 39, 40, 45, 50, 52, 60, 65, 72, 75, 78, 90, 100, 104, 117, 120, 130, 150, 156, 180, 195, 200, 225, 234, 260, 300, 312, 325, 360, 390, 450, 468, 520, 585, 600, 650, 780, 900, 936, 975, 1170, 1300, 1560, 1800, 1950, 2340, 2600, 2925, 3900, 4680, 5850, 7800, 11700 (不包含23400本身)

71 有一个除数的总数。最小的除数是2 和最高的11700 。所以预期的输出将是：

get_num([2,13,2,5,2,5,3,3]) == [23400, 71, 2, 11700]

题目难度：一般
题目来源： Following the Paths of Numbers Through Prime Factorization| Codewars 

def get_num(arr):
    # your code here
    return []
assert get_num([2,3,5,5]) == [150, 11, 2, 75]
assert get_num([2,3,3,3,7]) == [378, 15, 2, 189]
assert get_num([3,3,3,11]) == [297, 7, 3, 99]
assert get_num([2,13,2,5,2,5,3,3]) == [23400, 71, 2, 11700]
2

image
image1225×91 5.28 KB

3 
def get_num(arr: list) -> list:
    fresult = {}
    lresult = []
    sum_num = 1
    for i in arr:
        if i not in fresult.keys():
            fresult[i] = 1
        else:
            fresult[i] += 1
    for i in fresult:
        sum_num *= pow(i, fresult[i])
    for i in range(2, sum_num):
        if sum_num % i == 0:
            lresult.append(i)
            # 如果除数含1，需加1，不含1则不需要加1
    return [sum_num, len(lresult) + 1, min(lresult), max(lresult)]
4 
import math


def get_num(arr: list):
    number = 1
    number_sum = 0
    number_list = [i ** arr.count(i) for i in set(arr)]
    for t in number_list:
        number *= t
    for i in range(2, int(math.sqrt(number) + 1)):
        if number % i == 0:
            number_sum += 1
    return [number,number_sum*2+1,min(arr),int(number/min(arr))]
5 
from collections import Counter
from functools import reduce


def get_num(arr):
    ##先算出乘积
    tmp_dict=Counter(arr) ##统计每个元素重复出现的次数，返回一个字典
    tmp_mult=[i**tmp_dict.get(i) for i in tmp_dict.keys() ]##得出每个数**重复出现次数
    mult=reduce(lambda x,y:x*y,tmp_mult)##累计乘积
##总除数的个数
    tmp_chushu=[n for n in range(2,mult) if mult%n==0]
   
    num_chushu=len(tmp_chushu)
##最小数
    min_num=min(tmp_chushu)
##最大数
    max_num=max(tmp_chushu)

    return [mult, num_chushu, min_num, max_num]
6 
def get_num(arr):
    first_num = 1
    for i in arr:
        first_num *= i
    res_list = []
    for i in range(2, first_num):
        if first_num % i == 0:
            res_list.append(i)
    return [first_num, len(res_list) + 1, min(res_list), max(res_list)]


assert get_num([2, 3, 5, 5]) == [150, 11, 2, 75]
assert get_num([2, 3, 3, 3, 7]) == [378, 15, 2, 189]
assert get_num([3, 3, 3, 11]) == [297, 7, 3, 99]
assert get_num([2, 13, 2, 5, 2, 5, 3, 3]) == [23400, 71, 2, 11700]
7 
def get_num(arr):
    arr1=[(i,arr.count(i)) for i in set(arr)]
    res_list=[]
    n_list=[]
    n_value=[j[0]**j[1] for j in arr1]
    n=1
    for k in range(len(n_value)):
        n*=n_value[k]
    for l in range(1,n):
        if n%l==0:
            n_list.append(l)
    res_list.append(n)
    res_list.append(len(n_list))
    res_list.append(n_list[1])
    res_list.append(n_list[-1])
    return res_list

assert get_num([2,3,5,5]) == [150, 11, 2, 75]
assert get_num([2,3,3,3,7]) == [378, 15, 2, 189]
assert get_num([3,3,3,11]) == [297, 7, 3, 99]
assert get_num([2,13,2,5,2,5,3,3]) == [23400, 71, 2, 11700]