hogwarts
2022 年6 月 13 日 02:03
1
【示例】
题目难度:中等codewars-count '9’s from 1 to n
def solution(n: int)-> int:
# your code here
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
assert solution(279) == 48
# 进阶
assert solution(99999) == 50000
assert solution(565754) == 275645
先来个最low的实现
import re
def solution(n: int) -> int:
# your code here
count = 0
for i in range(1,n+1):
num = len(re.findall("9", str(i)))
count += num
return count
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
joyoko
2022 年6 月 13 日 04:34
3
def solution(n: int) -> int:
# your code here
result = 0
for i in range(1, n + 1):
count = str(i).count('9')
result += count
return result
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
1 个赞
xiaopeng
2022 年6 月 13 日 04:44
4
def solution(n: int) -> int:
# your code here
str_n = str(n)
carry_num = 1
count = 0
nine_num = 0
if int(str_n[-1]) >= 9:
count += 1
str_n = str_n[:-1]
while (True):
if len(str_n) == 0:
break
count += int(str_n[-1])*(carry_num*10**(carry_num-1))
if str_n[-1] == '9':
nine_num+=int(str(n)[len(str_n):]) + 1
str_n = str_n[:-1]
carry_num+=1
count+= nine_num
return count
def solution(n:int) -> int:
count = 0
for i in range(1,n+1):
count += str(i).count('9')
return count
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
def solution(n: int) -> int:
lens = len(str(n)) # 目标数字长度
if lens == 1:
return 1 if n == 9 else 0 # 递归结束条件
base = 10 ** (lens - 1) # 辅助数字
nines = (lens - 1) * 10 ** (lens - 2)
d, m = divmod(n, base) # 商数和除数
value = d * nines + solution(m) # 递归计算对应数量
if d == 9:
value += m + 1 # 单独处理9开头的
return value
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
# 进阶
assert solution(99999) == 50000
assert solution(565754) == 275645
解释:
第一步,总结规律,可以推断出:
个位:当为9时1个,其他0个
十位(10): 1个
百位(100): 20个
千位(1000): 300个
万位(10000): 4000个
也就是说,多位数中,某个位置上包含9的数字个数是: (长度 - 1) * 10 ** (长度 - 2),备用。
第二步,将目标数字拆解,分别统计每个位置上获取对应含9的数量。
可以借用divmod()函数,会同时得到商(整除部分)和余数(除不尽部分)。
另外注意,需要特殊处理下开头本身带9的数字,例如999,每个位置上额外加上对应余数和自身1个即可。比如考虑900的时候,其实只会统计0~899中9的个数,因为首位是9,其他位置任何数字都可以组成含9的组合,因此还要加上余数99个,另外还有首位自身1个。
1 个赞
zzh
2022 年6 月 14 日 02:10
8
def solution(n: int)-> int:
assert solution(8) == 0
def solution(n):
result = 0
for i in range(1,n+1):
result += str(i).count('9')
return result
def solution(n: int)-> int:
cout = 0
for i in range(n+1):
cout += str(i).count('9')
return cout
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
assert solution(279) == 48
# 进阶
assert solution(99999) == 50000
assert solution(565754) == 275645
规律:
个位:当为9时1个,其他0个
十位(10): 1个
百位(100): 20个
千位(1000): 300个
万位(10000): 4000个
......
def solution(n: int) -> int:
s = str(n) # 转成字符串
total = 0
for i in range(len(s)):
base = i*10**(i-1) # 找规律
total += int(s[~i])*int(base) # 倒着取数
if s[i] == "9":
# 单独处理字面含9的情况
total += int(s[i+1::] or 0) + 1
return total
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
assert solution(279) == 48
assert solution(99999) == 50000
assert solution(565754) == 275645
1 个赞
Olivia
2022 年6 月 15 日 03:49
13
def solution(n: int)-> int:
count = 0
for i in range(n+1):
count = count + str(i).count("9")
return count
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
assert solution(279) == 48
assert solution(99999) == 50000
assert solution(565754) == 275645
joyoko
2022 年6 月 17 日 06:49
15
数据量不大的情况下这个解法没毛病,不过数据量大了,百里老师那个推导出来的数学模型才是最优解。【每日一题20220613】9的时代 - #7,来自 Amoyshmily
def solution(n:int)->int:
count_9 = 0
for i in range(1,n+1):
count_9 += str(i).count('9')
return count_9
assert solution(8) == 0
assert solution(10) == 1
assert solution(100) == 20
assert solution(279) == 48
#进阶
assert solution(99999) == 50000
assert solution(565754) == 275645
def solution(n: int)-> int:
return ''.join([str(i) for i in range(1,n+1)]).count('9')
def solution(n: int)-> int:
# your code here
s = 0
for i in range(1, n+1):
if "9" in str(i):
for j in str(i):
if j == "9":
s += 1
return s
lekaixin
2024 年3 月 12 日 09:49
19
def solution(n: int) -> int:
lenn=len(str(n))
if lenn==1:
if n==9:
return 1
else:
return 0
base=(lenn-1)*10**(lenn-2)
shang=n//(10**(lenn-1))
yu=n%(10**(lenn-1))
res=shang*base+solution(yu)
if shang==9:
res+=(yu+1)
return res
assert solution(8) == 0
assert solution(10) == 1
assert solution(98) == 18
assert solution(100) == 20
assert solution(279) == 48
assert solution(998) == 297
assert solution(999) == 300
assert solution(1000) == 300
assert solution(10000) == 4000
# 进阶
assert solution(99999) == 50000
assert solution(565754) == 275645
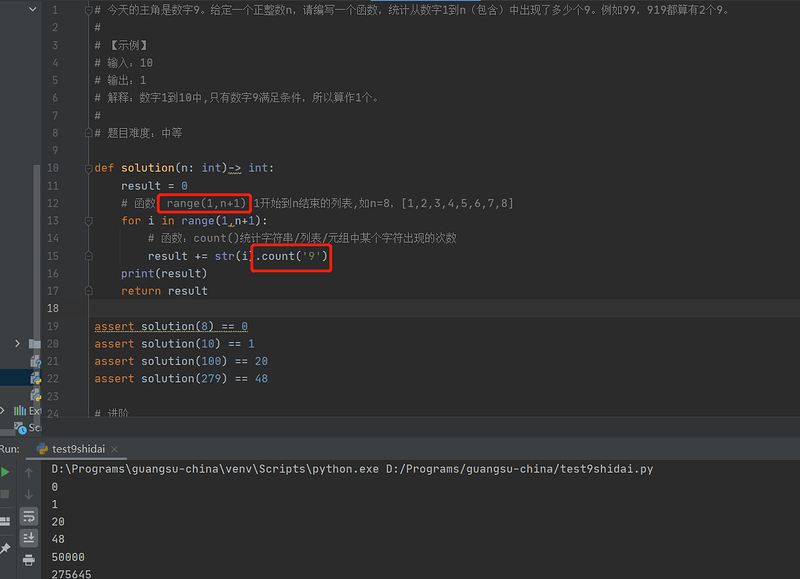
![]() 今天的主角是数字9。给定一个正整数n,请编写一个函数,统计从数字1到n(包含)中出现了多少个9。例如99,919都算有2个9。
今天的主角是数字9。给定一个正整数n,请编写一个函数,统计从数字1到n(包含)中出现了多少个9。例如99,919都算有2个9。