剑指 Offer 60. n个骰子的点数
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
示例 1:
输入: 1
输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
限制:
- 1 <= n <= 11
来源:力扣(LeetCode)
链接:力扣
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
一解
动态规划。假设已知 n - 1 个骰子的所有解 f(n - 1),此时添加一个骰子,求第 n 个骰子时,和为 x 的概率 f(n, x):
-
添加的骰子点数为 1 时:
x = x-1 + 1,前 n-1 个骰子的点数和应为 x-1 -
添加的骰子点数为 2 时:
x = x-2 + 2,前 n-1 个骰子的点数和应为 x-2 -
…
-
添加的骰子点数为 6 时:
x = x-6 + 6,前 n-1 个骰子的点数和应为 x-6
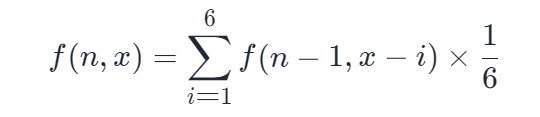
class Solution:
def dicesProbability(self, n: int) -> List[float]:
dp = [1/6]*6
for i in range(2, n + 1):
tmp = [0]*(5*i + 1)
# f(n-1, k) 影响 f(n, k + 0), f(n, k + 1)+...+ f(n, k + 6)
for j in range(len(dp)):
for k in range(6):
tmp[j+k] += dp[j] / 6
dp = tmp
return dp
