剑指Offer47-礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
提示:
-
0 < grid.length <= 200
-
0 < grid[0].length <= 200
来源:力扣(LeetCode)
链接:力扣
一解
使用动态规划,设dp[i][j]表示从位置 0, 0 到位置 i, j 的最大价值:
-
动态方程:
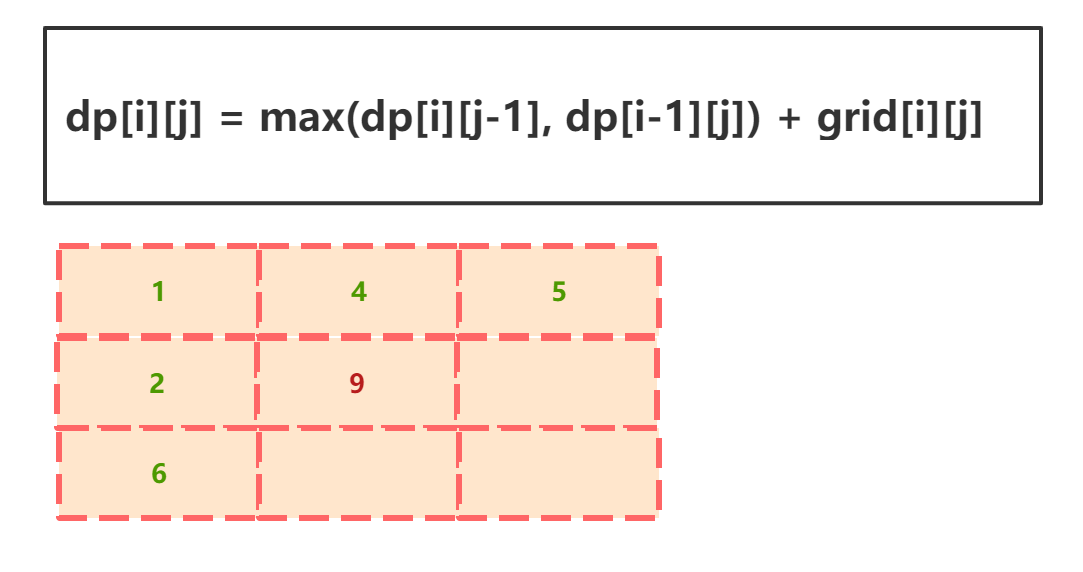
dp[i][j] = max(dp[i][j-1], dp[i-1][j]) + grid[i][j] -
初始状态:
dp[0][0] = grid[0][0] -
返回值:
dp[m-1][n-1]
当i==0或j==0时:
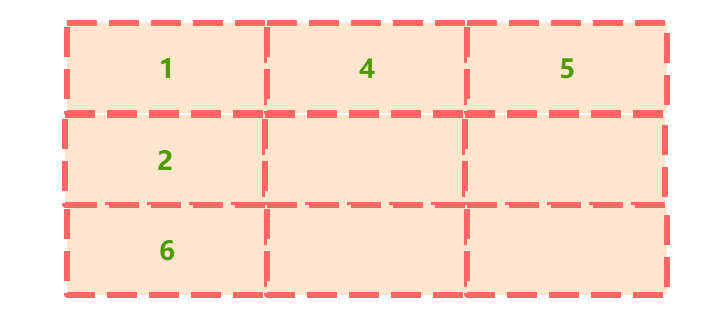
当i=1, j=1时:
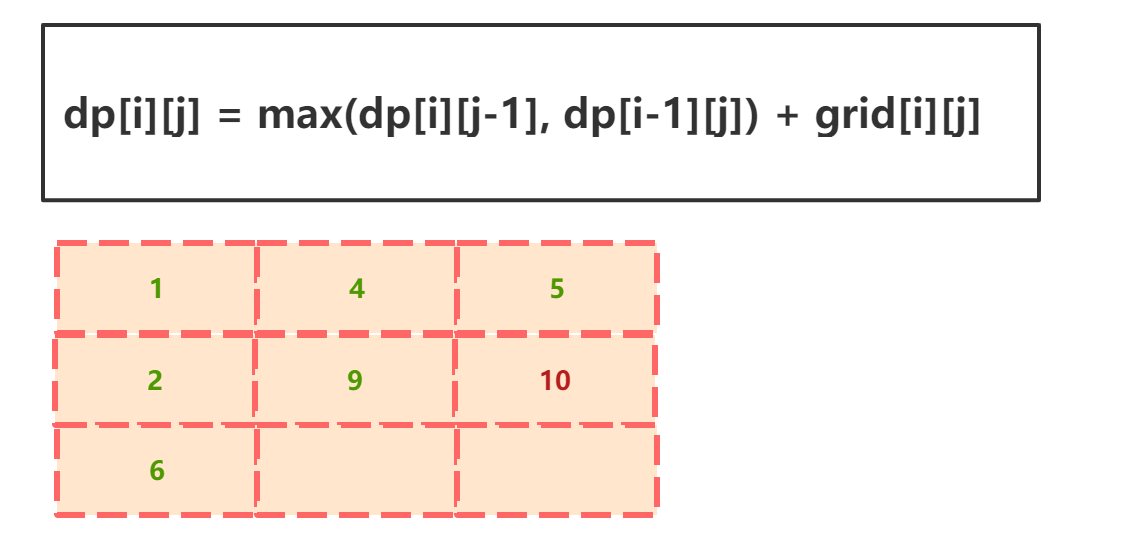
当i=1, j=2时:
当i=2, j=1时:
当i=2, j=2时:
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
dp = [[0 for _ in range(n)] for _ in range(m)]
dp[0][0] = grid[0][0]
for i in range(1, n):
dp[0][i] = dp[0][i - 1] + grid[0][i]
for i in range(1, m):
dp[i][0] = dp[i - 1][0] + grid[i][0]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = max(dp[i][j - 1], dp[i-1][j]) + grid[i][j]
return dp[m-1][n-1]
二解
原理同一解,为了节省空间,可利用 grid 替代 dp :
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
for i in range(len(grid)):
for j in range(len(grid[0])):
if i == 0 and j == 0: continue
if i == 0: grid[i][j] += grid[i][j - 1]
elif j == 0: grid[i][j] += grid[i - 1][j]
else: grid[i][j] += max(grid[i][j - 1], grid[i - 1][j])
return grid[-1][-1]
三解
原理同一解。二解的 i=0 或 j=0 的情况占少数,但每次循环都要进行判断,因此,可先初始化矩阵第一行和第一列,再开始遍历递推。:
class Solution:
def maxValue(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
for i in range(1, n): grid[0][i] += grid[0][i-1]
for i in range(1, m): grid[i][0] += grid[i-1][0]
for i in range(1, m):
for j in range(1, n):
grid[i][j] += max(grid[i][j - 1], grid[i-1][j])
return grid[m-1][n-1]