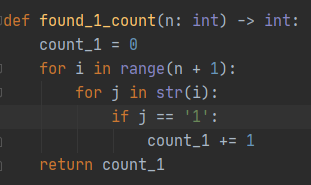
剑指Offer43-1~n 整数中1出现的次数
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
输入:n = 12
输出:5
示例 2:
输入:n = 13
输出:6
限制:
- 1 <= n < 2^31
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/1nzheng-shu-zhong-1chu-xian-de-ci-shu-lcof\
一解
1~n这n个整数的十进制表示中1出现的次数,相当于个位 1 数量 + 十位 1 数量 + 百位 1 数量 + ..,以 1139 举例,求十位 1 数量:
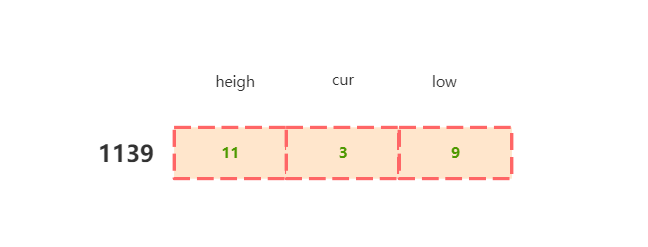
当 cur 为 3 时,其高位是 11 ,低位是 9 ,求十位为 1 的数量。
根据题目要求,需要从1~n中寻找十位为 1 的数字,即1~1139,因此该数字特征如下:
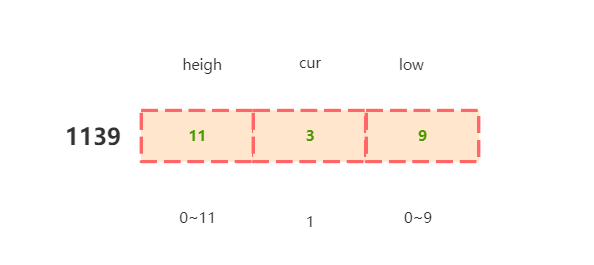
heigh 高位可以是 0~11 任意数字,cur 为 1 ,low 低位可以是 0~9 任意数字,总数量为(high+1)×digit,其中 digit 表示位因子,个位为 1 ,十位为 10 ,百位为 100 :
再比如,求 11377 百位 1 的数量:
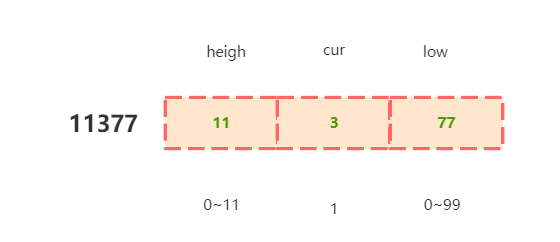
总数量也是(high+1)×digit。
因此得出以下推论:
-
当 cur = 0 时:high×digit
-
当 cur = 1 时:high×digit+low+1
-
当 cur > 1 时:(high+1)×digit
class Solution:
def countDigitOne(self, n: int) -> int:
digit, res = 1, 0
# 当 cur 为个位
high, cur, low = n//10, n%10, 0
# 当 high 和 cur 同时为 0 时,即计算完最高位时退出循环
while high != 0 or cur != 0:
if cur == 0: res += high*digit
elif cur == 1: res += high*digit + low + 1
else: res += (high + 1)*digit
low += cur*digit # 利用上一次的 cur 和 low 计算本次的 low
cur = high % 10
high //= 10
digit *= 10
return res