多叉树与红黑树

ruotongyu · 2021 年4 月 16 日 02:49

引言

时间复杂度分析

树的插入，删除，查找的时间复杂度与树的高度成正比： O(高度) == O(最大层数 - 1) ，最符合需求的就是完全二叉树，来看下完全二叉树的最大高度：

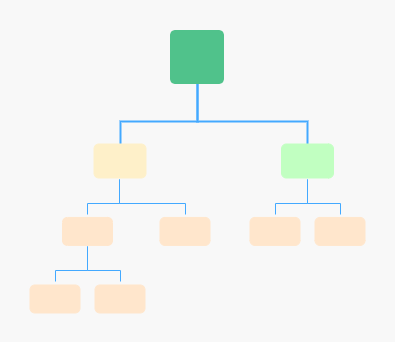
完全二叉树

完全二叉树除最后一层，每层结点数：1, 2, 4,…, 2^k-1
最后一层：1~2^(L-1)
完全二叉树的结点数 n ：

n >= 1+2+4+8+…+2^L-2 + 1

n <= 1+2+4+8+…+2^L-2 + 2^L-1

利用等比数列求和公式：

L 的范围是 [log₂(n+1), (log₂n) +1]。完全二叉树的层数 <= (log₂n) +1 ，其高度小于等于 log₂n

二叉查找树会出现树的高度过高，从而导致各个操作的效率下降，比如下图只有右孩子的树（退化成了链表）：

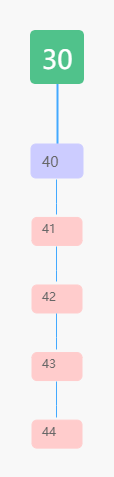
二叉树结构 (9)

为避免这种情况，一般选用平衡二叉查找树：红黑树。

什么是平衡二叉查找树？

平衡二叉树：任意节点左右子树的高度差 <= 1：

平衡二叉树：

平衡二叉树

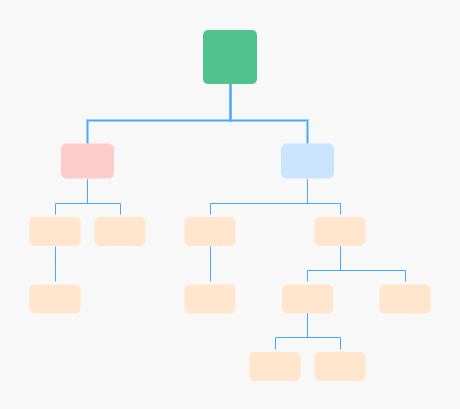
非平衡二叉树

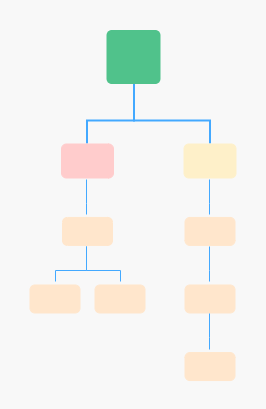
早期的 AVL 树是平衡二叉树 + 查找 = 平衡二叉查找树。

但为了实际应用，后续的树都没遵从平衡树的定义（比如红黑树），只要树的高度不比 log₂n 大很多，都符合定义。

红黑树的英文是 Red-Black Tree，简称 R-B Tree。

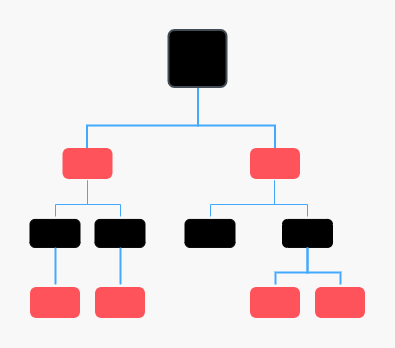
二叉树结构

为什么红黑树的高度可以稳定地趋近 log₂n ？

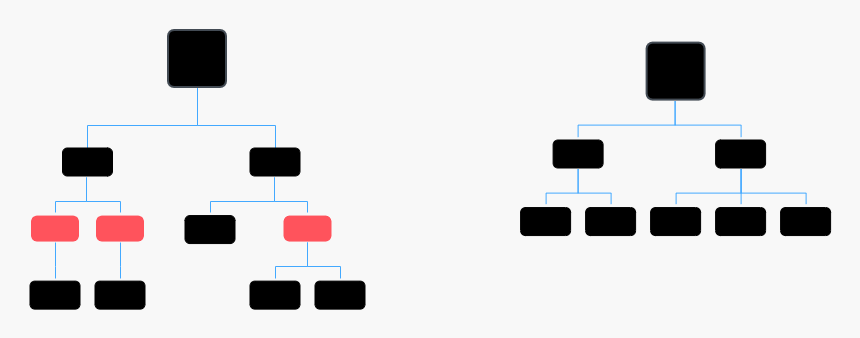
将红色节点删除，变成下图（四叉树），由于每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点，于是四叉树可以转换成完全二叉树，于是仅包含黑色节点的四叉树的高度，比包含相同节点个数的完全二叉树的高度还要小。

把红色节点加回去，由于红色节点不能相邻（红色数量 ~= 黑色数量）。红黑树的高度近似 2log₂n。