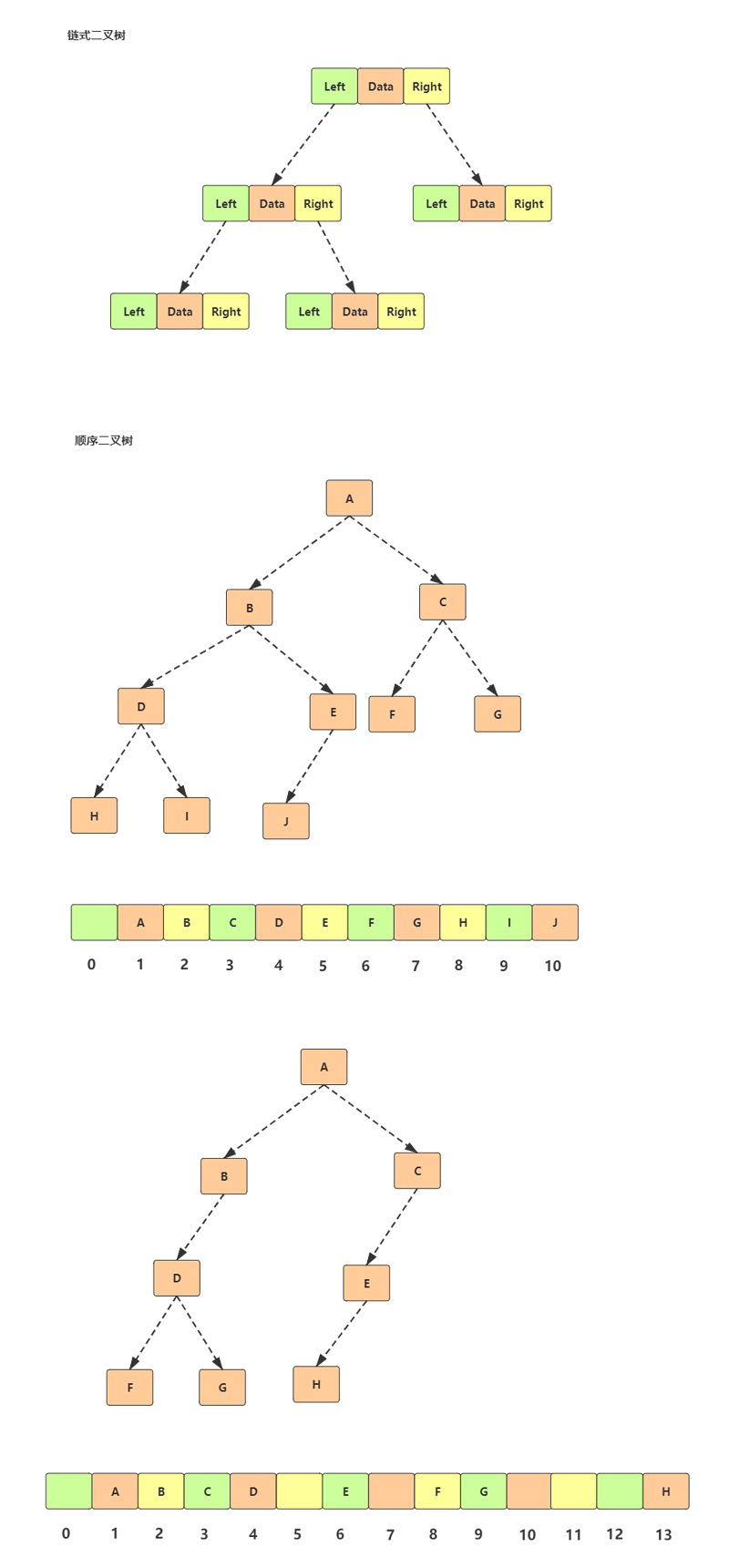
树的基本术语
父节点,子节点: A 和B
兄弟节点:D E J
根节点:A
叶节点:G I
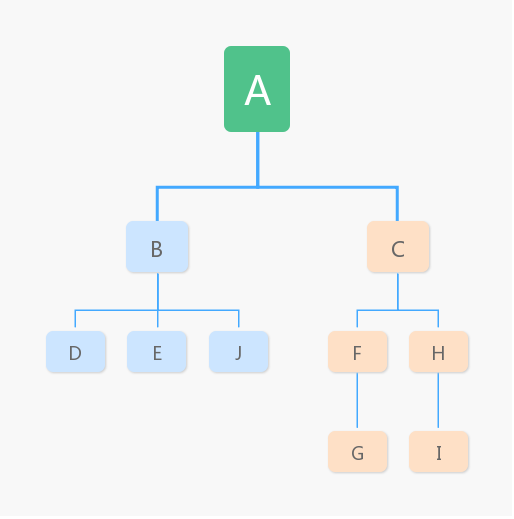
- 节点高度:节点到叶节点的最长路径(边数)
- 节点深度:根节点到这节点所经历的边的个数
- 节点的层数:节点的深度 + 1
- 树高度:根节点的高度
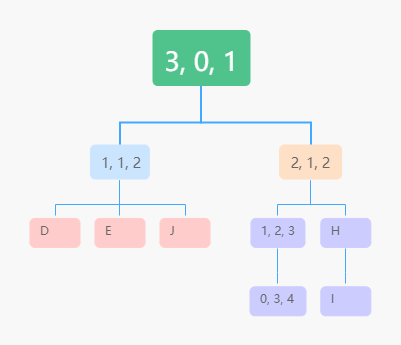
- 节点的高度:一个人量身体各部位长度,从脚下拉尺到各部位(腿长)
- 节点深度:量水中物品的深度,从水面拉尺到水中的宝藏
- 节点的层数:尺子从 1 开始计数
- 树高度:头到脚的高度
二叉树
最多有两个叉的树。
满二叉树:叶子节点全在最底层,除了叶子节点之外,每个节点都有左右两个子节点。
完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。
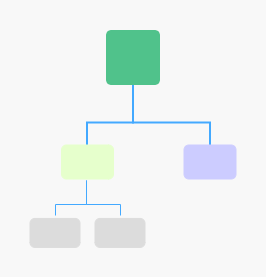
满二叉树和完全二叉树的意义是什么?
- 节点 X 在数组下标 i
- 左子节点:2 * i
- 右子节点:2 * i + 1
- 父节点:i/2
二叉树的遍历
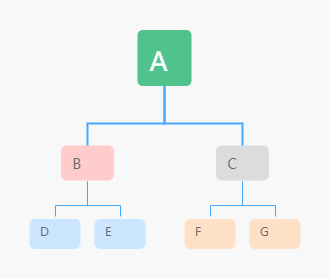
根据节点打印的顺序分前,中,后。比如:
- 前序遍历:节点 → 左子树 → 右子树。A->B->D->E->C->F->G
- 中序遍历:左子树 → 节点 → 右子树。D->B->E->A->F->C->G
- 后序遍历:左子树 → 右子树 → 节点。D->E->B->F->G->C->A
递推关系式:
前序遍历的递推公式:
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式:
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式:
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
代码:
void preOrder(Node* root) {
if (root == null) return;
print root // 此处为伪代码,表示打印root节点
preOrder(root->left);
preOrder(root->right);
}
void inOrder(Node* root) {
if (root == null) return;
inOrder(root->left);
print root // 此处为伪代码,表示打印root节点
inOrder(root->right);
}
void postOrder(Node* root) {
if (root == null) return;
postOrder(root->left);
postOrder(root->right);
print root // 此处为伪代码,表示打印root节点
}
复杂度:
O(n):遍历操作的时间复杂度,跟节点的个数 n 成正比
二叉查找树
左子树每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
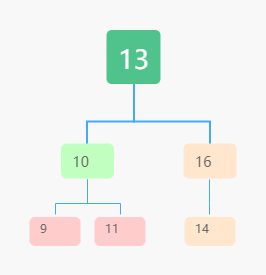
查找
根节点
-比之小> 左子树中递归查找。
-比之大> 右子树中递归查找。
插入
- 从根节点开始比较,如果比之大,并且节点右子树为空,就将新数据插到右子节点;
- 如果不为空,就再递归遍历右子树,查找插入位置。
- 如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置。
- 如果不为空,就再递归遍历左子树,查找插入位置。
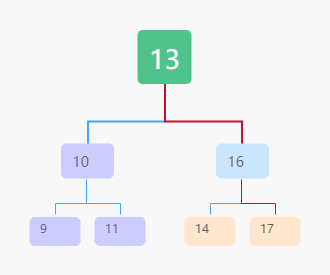
删除
情况一:要删除的节点没有子节点
只需要直接将父节点中,指向要删除节点的指针置为 null。比如图中的删除节点 55。
情况二:如果要删除的节点只有一个子节点(只有左子节点或者右子节点),
只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。
情况三:如果要删除的节点有两个子节点
- 找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。
- 然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。
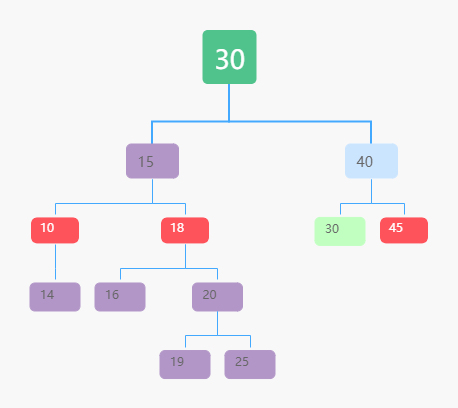

取巧方法:将要删除的节点标记为“已删除”。
重要特性
中序遍历二叉查找树,可以得到有序的数据序列,时间复杂度是 O(n)。因此,二叉查找树又称二叉排序树。
class BinarySearchTree:
def __init__(self) -> None:
self.tree = None
class Node:
def __init__(self, data) -> None:
self.data = data
self.left = None
self.right = None
def insert(self, value):
# 如果是根结点,直接插入
if self.tree is None:
self.tree = self.Node(value)
return
p = self.tree
while p is not None:
if value > p.data:
if p.right is None:
p.right = self.Node(value)
return
p = p.right
elif value < p.data:
if p.left is None:
p.left = self.Node(value)
return
p = p.left
def find(self, value):
p = self.tree
while p is not None:
if value > p.data:
p = p.right
elif value < p.data:
p = p.left
else:
return p
return None
def delete(self, value):
p = self.tree
pp = None
while p is not None and p.data != value:
pp = p
if value > p.data:
p = p.right
elif value < p.data:
p = p.left
if p is None:
return
if p.left is not None and p.right is not None:
tmp_p = p.right
tmp_pp = p
# 找要删除结点的右子树中的最小值
while tmp_p.left is not None:
tmp_pp = tmp_p
tmp_p = tmp_p.left
p.data = tmp_p.data
p = tmp_p
pp = tmp_pp
if p.left is not None:
child = p.left
elif p.right is not None:
child = p.right
else:
child = None
# 删除根结点
if pp is None:
self.tree = child
elif pp.left is p:
pp.left = child
elif pp.right is p:
pp.right = child
def pre_order(self, node):
if node is None:
return
print(node.data)
self.pre_order(node.left)
self.pre_order(node.right)
def in_order(self, node):
if node is None:
return
self.in_order(node.left)
print(node.data)
self.in_order(node.right)
def post_order(self, node):
if node is None:
return
self.post_order(node.left)
self.post_order(node.right)
print(node.data)
def test_binary_search_tree():
binary_search_tree = BinarySearchTree()
data = [1, 10, 20, 40, 13]
for i in data:
binary_search_tree.insert(i)
assert 20 == binary_search_tree.find(20).data
binary_search_tree.delete(20)
assert binary_search_tree.find(20) is None
# 1 10 40 13
binary_search_tree.pre_order(binary_search_tree.tree)
print("-----------------------")
# 1 10 13 40
binary_search_tree.in_order(binary_search_tree.tree)
print("-----------------------")
# 13 40 10 1
binary_search_tree.post_order(binary_search_tree.tree)
if __name__ == '__main__':
test_binary_search_tree()