4.递归计算

ruotongyu · 2021 年4 月 9 日 00:34

什么是递归？

递归应用非常广泛，比如 DFS 深度优先搜索、前中后序二叉树遍历等等。

假设一群人在排队，你不清楚自己前面有多少人，可以问前面的人：

但你前面也不清楚，整体过程就是递归：

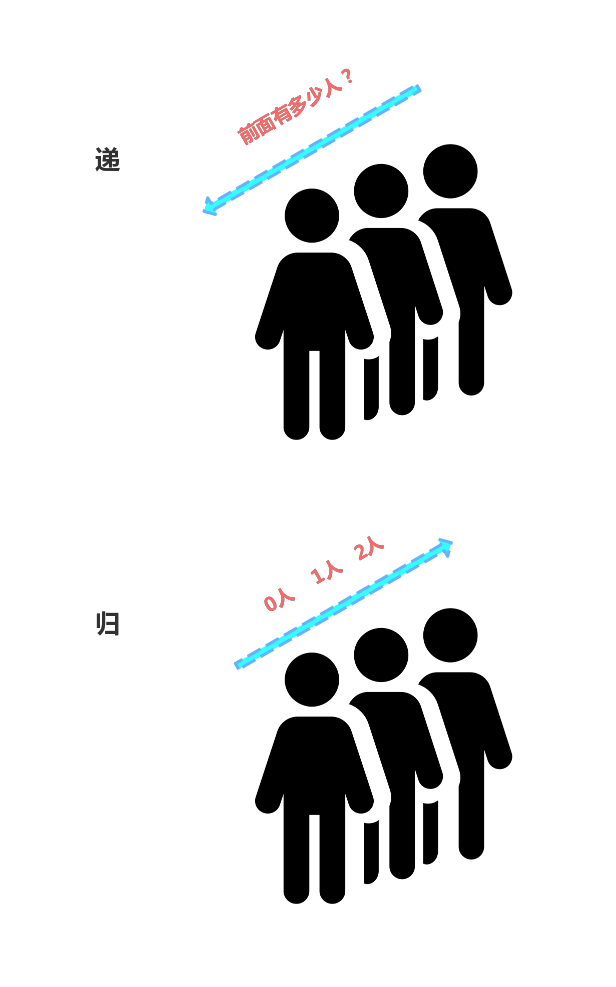
如果用递推公式描述：

f(n)=f(n-1)+1 其中，f(1)=1


int f(int n) {
  if (n == 1) return 1;
  return f(n-1) + 1;
}

什么情况可以使用递归？

一个问题可以拆分成子问题.
这些问题求解思路相同（数据规模不同）
拥有终止条件

来看一个问题：

假如 n 个台阶（n >= 3），每次可以走 1 或 2 个台阶，走完 n 个台阶有多少种走法？
比如有 3 个台阶，可以 1，2 或者 2，1 ：

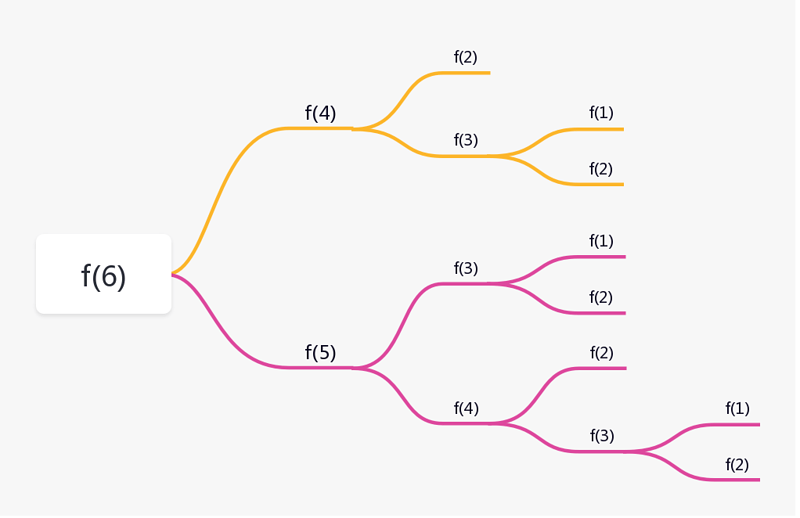
f(n) = f(n-1)+f(n-2)  其中，f(1)=1，f(2)=2


int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  return f(n-1) + f(n-2);
}

常见问题

深度问题

重复计算问题


public int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  
  // hasSolvedList可以理解成一个Map，key是n，value是f(n)
  if (hasSolvedList.containsKey(n)) {
    return hasSolvedList.get(n);
  }
  
  int ret = f(n-1) + f(n-2);
  hasSolvedList.put(n, ret);
  return ret;
}

内存开销问题


int f(int n) {
  if (n == 1) return 1;
  return f(n-1) + 1;
}

空间复杂度：O(n)

将递归改写为非递归


int f(int n) {
  int ret = 1;
  for (int i = 2; i <= n; ++i) {
    ret = ret + 1;
  }
  return ret;
}

int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  
  int ret = 0;
  int pre = 2;
  int prepre = 1;
  for (int i = 3; i <= n; ++i) {
    ret = pre + prepre;
    prepre = pre;
    pre = ret;
  }
  return ret;
}

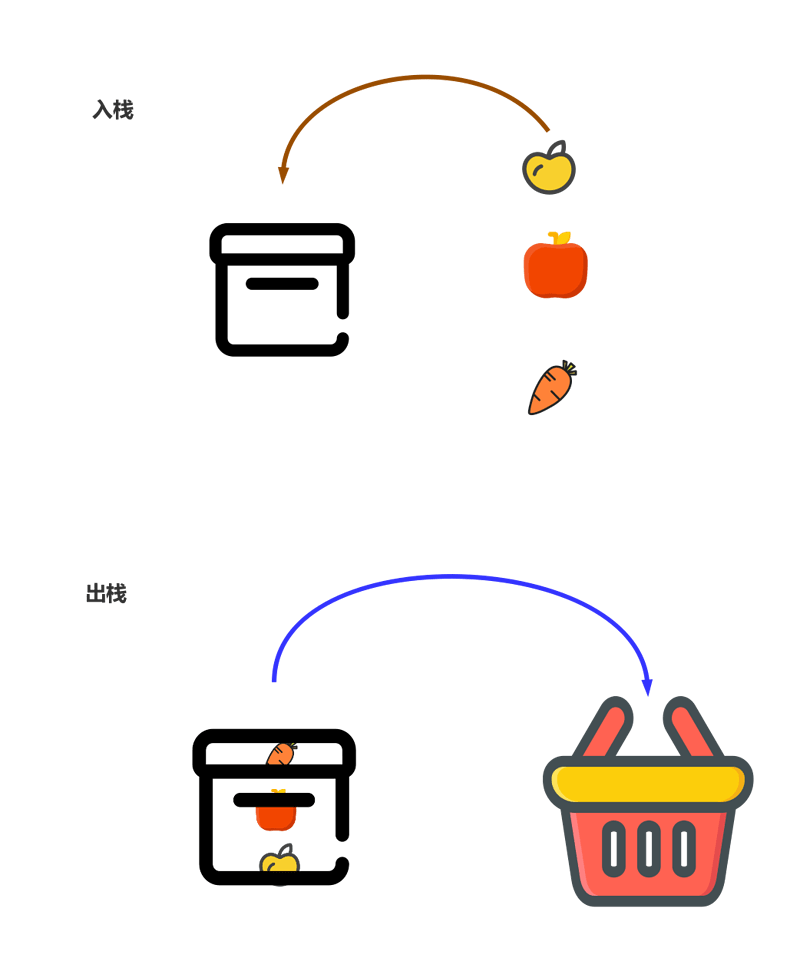
原理：函数调用底层原理是栈，可以利用 for 循环模拟入栈和出栈操作