地址
难度
简单
题目
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
- 1 <= numRows <= 30
思路
- 递归
递归方法总而言之就是抓住三点:
- 找整个递归的终止条件
- 找返回值
- 一次递归需要如何操作
找整个递归的终止条件
分析一下题目,递归到numRows = 0 时或者numRows = 1时都可以终止,因为第一行比较特殊,只有一个1,可以将其当成整个递归的终止条件,当numRows = 1时,就可以终止递归向下返回值了。
找返回值
题目要我们求的是整个杨辉三角的所有数,那最后递归得到的应该就是 List<List> (题目给定),也就是每递归完一层,就更新完List并返回即可,最后递归完成就是我们要的答案。
一次递归需要如何操作
只需要关注一次递归即可,因为每一层递归的过程都是一样的,只需要找到最上层的递归的规律,就可以了。
class Solution {
public List<List<Integer>> generate(int numRows) {
//存储要返回的杨辉三角
List<List<Integer>> dg = new ArrayList<>();
//若0行,则返回空
if(numRows == 0){
return dg;
}
//递归出口,这是第一步!找到出口
if(numRows == 1){
dg.add(new ArrayList<>());
dg.get(0).add(1);
return dg;
}
//递归,注意返回值!!!这是第二步
dg = generate(numRows-1);
//一级递归要做啥,我们可以看第二行到第三行需要做啥
//首先是要申请一个list来存储第三行,然后通过第二行得到第三行
//第三行的首尾为1是确定了的,然后就是中间的数如何得到
//通过观察很容易拿到for循环里面的式子
//最后别忘了返回值!!!
List<Integer> row = new ArrayList<>();
row.add(1);
for(int j = 1;j < numRows - 1;j++){
row.add(dg.get(numRows-2).get(j-1) + dg.get(numRows-2).get(j));
}
row.add(1);
dg.add(row);
return dg;
}
}
- 动态规划
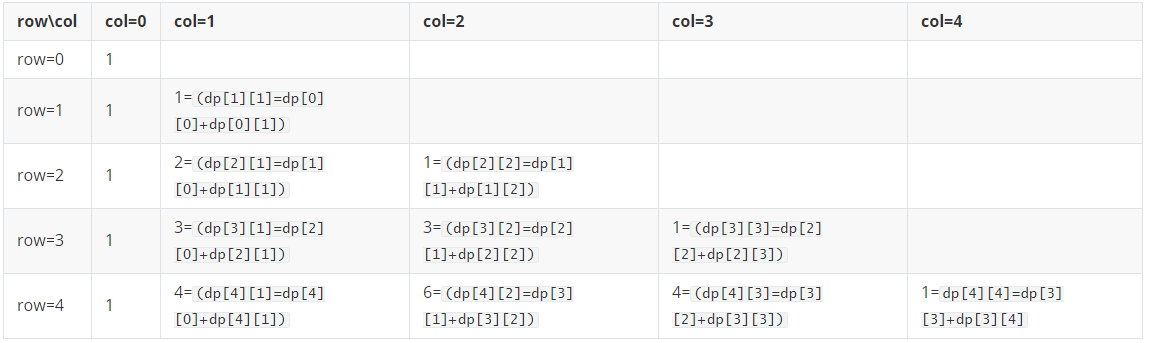
用一个二维数组dp[numRows][numRows]保存每一次动态规划的结果
1.令dp[0][0]=1(第一列)
2.根据以下表格找到规律
得到如下规律(以下情况均为列数大于1)if(col==0){ dp[row][col]=1 } else { dp[row][col]=dp[row-1][col-1]+dp[row-1][col] }
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> list = new ArrayList<List<Integer>>();
for (int i = 0; i < numRows; i++) {
List<Integer> tList = new ArrayList<Integer>();
for (int j = 0; j <= i; j++) {
if (j == 0 || i == j) {
tList.add(1);
} else {
tList.add(list.get(i - 1).get(j - 1) + list.get(i - 1).get(j));
}
}
list.add(tList);
}
return list;
}
}