在代码红线扫描业务中,会扫描出开发提交项目代码中的一些bug或者警告,开发会按需对其中一些进行修复。目前,扫描出的bug按照red、safe、block、serious、risk、warning、style、suggestion、normal顺序排列展示,且扫出的建议修复点比较多,小则几十,多则上千,但是从开发的修复情况来看,没有遵循这个顺序。
如果开发想要从扫描出的建议修复点中找到自己必须修复的,就必须从头看到尾,比较耗时。本方法就是通过以往开发对修改点的修复情况,来对新扫描出的建议修复点进行排序,从而提高开发修复的效率。
![]()
明确目标和评估方式
从上述需求来看,我们希望通过以往开发人员对bug修复情况,预测扫描出的bug修复的可能性,从而对新版本扫描出来的bug列表排序。即:回归问题。
回归算法常用评估有:
● explained_variance_score
● mean_absolute_error
● mean_squared_error
● r2_score
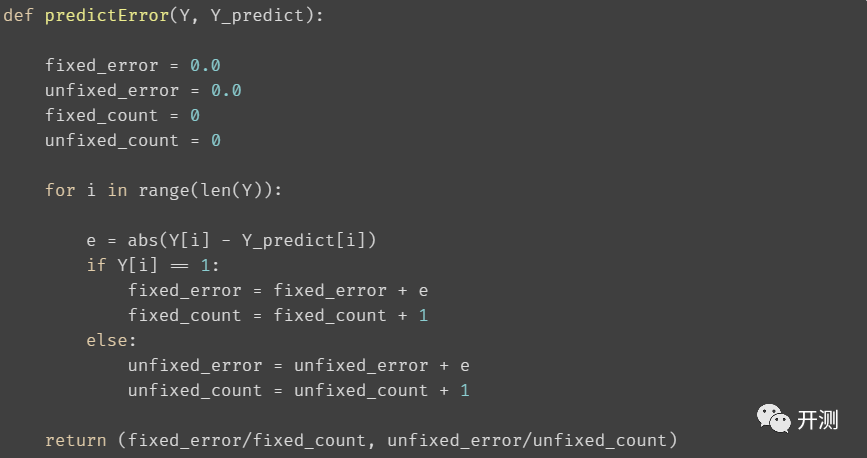
因为标签的值为 0或1,我们也想着重看一下,需要修改的样本预测值与实际值的误差:
![]()
特征的选择
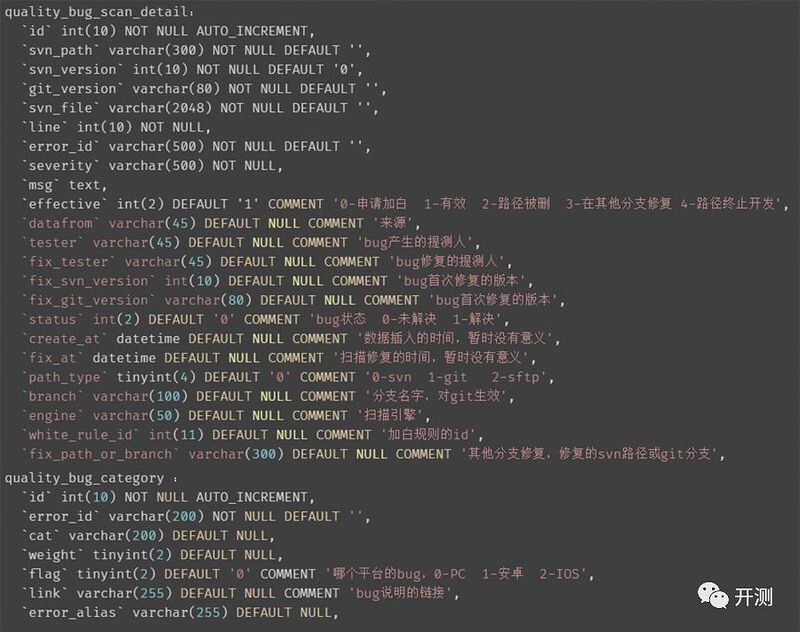
通过观察目前bug扫描相关的数据(如下图所示):
考虑到:
● 不同项目对bug的容忍程度不同;
● 不同提交版本,根据紧急程度也不一样;
● 不同bug威胁程度;
● 保持训练数据字段和最终预测能给出字段的一致性;
最终选择特征:
● svn_path:哪一个svn或git目录;
● svn_file:文件路径;
● error_id:错误的标题;
● msg: 错误描述;
● cat: 错误类型;
标签:
● status:是否被修复过,数值(0 | 1)
![]()
数据的清洗
因为业务逻辑和版本的迭代,会给存储在数据库中的数据带来一些脏数据,咱们需要了解业务逻辑结合数据的特点,对数据进行清洗。
例如:
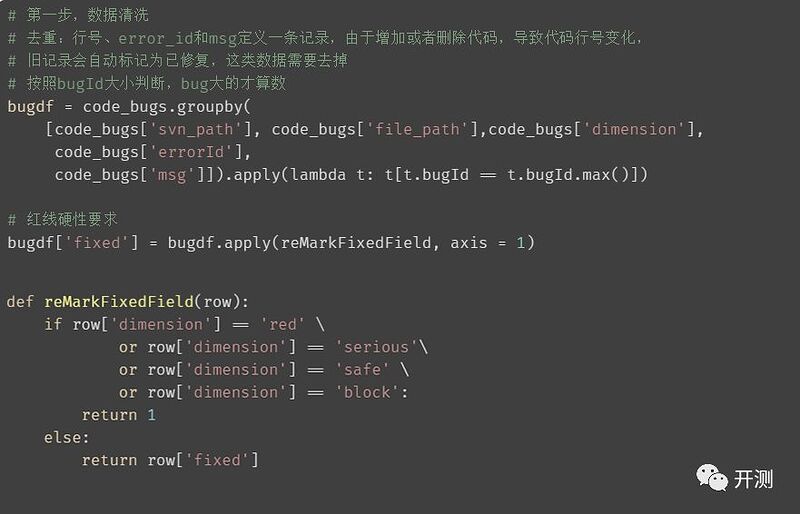
● 相同bug存在多条记录且标记不一致:
行号、error_id和msg定义一条记录,由于增加或者删除代码,导致代码行号变化,旧记录会自动标记为已修复;
加白后的bug,下次再扫描到时,也会标记为已修复;
● 正负样本比例严重失衡:
拆分训练集和测试集时需要均衡一下;
● 时间上的样本差异:
前期PC端的数据较多,多为C++代码,且使用svn存储;后期加入Android端数据,大量Java代码,且使用git的增多;
● 扫描出来的bug分类为red、serious、safe、block时,必须修改,这是红线扫描的硬性标准:因此需要将这类数据也标成修复状态;
![]()
特征数值化
在把数据扔入模型之前,需要先把刚才选取的特征进行数值化。
因为错误标题、错误类型、项目标识表示空间有限,且增长缓慢。所以可以考虑使用词典+计数的方式表示特征。
我们这里使用CountVectorizer帮我们计算词典:
例如错误类型特征的词典就可以得到:
在计算某条数据中错误类型对应数值数组时:
和错误类型这类特征相比,filePath这类由开发自定义定义,自由度大的特征在使用词典表示时容易出现词袋易膨胀,这时我们怎么办呢?
处理这类问题的解决方案有很多,在这里,我们采取压缩编码 – 哈希方案。
大家都知道,哈希是使用确定性函数将一个潜在的无界整数到有限整数范围[1,m],这样就能解决咱们词典膨胀的问题。但是也要注意这个方式也使特征失去了可解释性。
在处理路径类型数据(filePath\svnPath)时,为了能够让特征能够表达相同目录下文件的重要等级相似,所以这里我们对这类数据进行分段累加:
● 按/分割,再逐个组装。例如:/A/B/C, 分割后得到 [‘A’, ‘B’, ‘C’],组装后, [‘A’, ‘AB’, ‘ABC’];
● 通过simhash计算组装后得到的值表示特征;
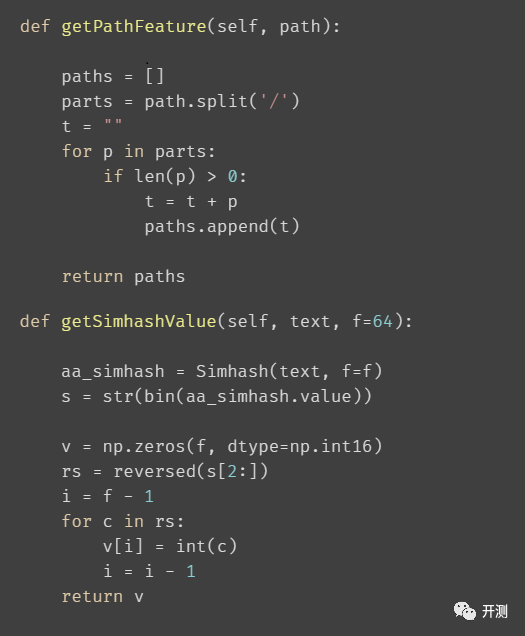
s1 = “/A/src/main/java/com/D/E”
s2 = “/B/src/main/java/com/D/E”
s3 = “/A/src/main/java/com/K/C/L”
s4 = “/A/src/main/java/com/D/F”
/A/src/main/java/com/D/E 与 /B/src/main/java/com/D/E 的差距:38
/A/src/main/java/com/D/E 与 /A/src/main/java/com/K/C/L 的差距:18
/A/src/main/java/com/D/E 与 /A/src/main/java/com/D/F 的差距:10
以s1为标准,计算海明距离,可以看出,这样的处理方式基本可以满足咱们的需求。
错误描述就直接采用空格分词,计算simhash表示。
![]()
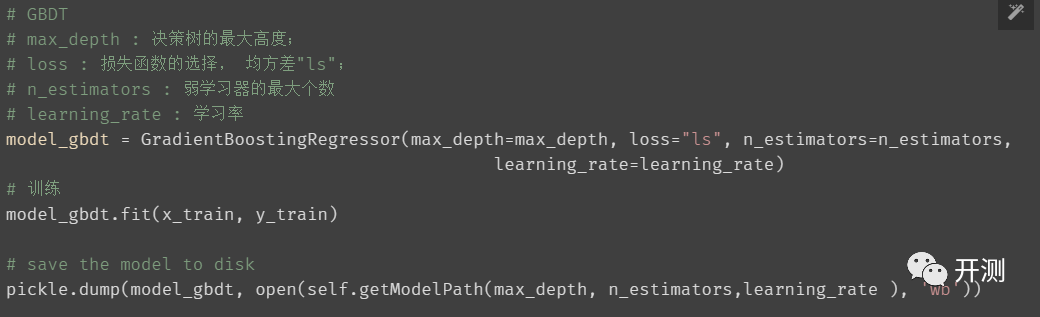
模型选择
回归算法:我们这里选择,决策树 - sklearn GBDT
![]()
模型调参
通过控制变量法,先粗粒度选定参数区间后,再细粒度组合调整,使用cross_val_score(交叉验证)的方式评估各组参数的优劣。
模型评估结果
explained_variance_score :0.9689144942213028
mean_absolute_error :0.00207038436776197
mean_squared_error :0.0016704427036573243
r2_score :0.9689142009849029
正例的平均误差:0.001031256933640255
负例平均误差:0.019266790713858478

长按二维码,关注官方微信公众号!