点击上方蓝字关注我们!
前言
经常听到研发面试基础题或者说基本功都包括算法题目,那常用的算法都有哪些?
小白们也很熟悉的:冒泡,归并,简单选择,归并,堆排序。
那它们区别是什么呢?需要好好梳理一下了。今天咱们就先瞅瞅感觉比较抽象的堆算法吧。
01
堆排序基本思想
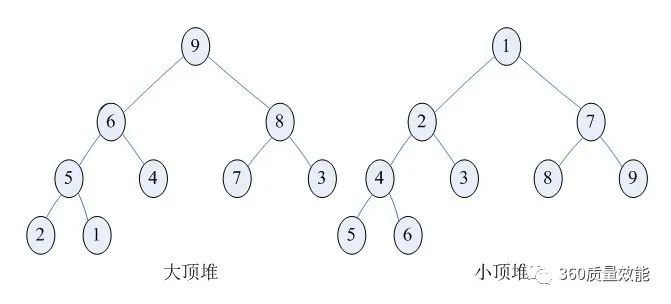
什么是堆?堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右子结点的值,称为小顶堆。
堆排序(Heap Sort)就是利用堆(假设利用大顶堆)进行排序的方法。它的基本思想是,将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的n-1个(0…n-1)序列重新构造成一个堆,这样就会得到n个元素中的次小值。如此反复执行,便能得到一个有序序列了。
问
好了简单介绍之后,也没觉得有啥记忆的功能啊?
答
其实堆是有记忆功能的,就是因为他自身的结构,每个结点的值都大于或等于其左右孩子结点的值(这是大顶堆,小顶堆则是每个结点的值都小于或等于其左右孩子结点的值),这就是记忆!当你将整个序列构建成一个堆之后,那么结点元素是比左右孩子大或者小的,这就是记忆!如果还是晕的,那么恭喜你,我在学习的过程中这个阶段的时候也是没想明白的,先看看实现吧!
02
堆排序实现
先看看核心代码
/**
* 堆排序
*
* @paramarr
*/
public void sort(int[] arr) {
System.out.println("初始序列状态: " + Arrays.toString(arr) + "\n");
intlen = arr.length;
//构建初始大顶堆
for (inti = len / 2 - 1; i>= 0; i--) {
System.out.println("构建初始大顶堆: " + i);
heapAdjust(arr, i, len - 1);
}
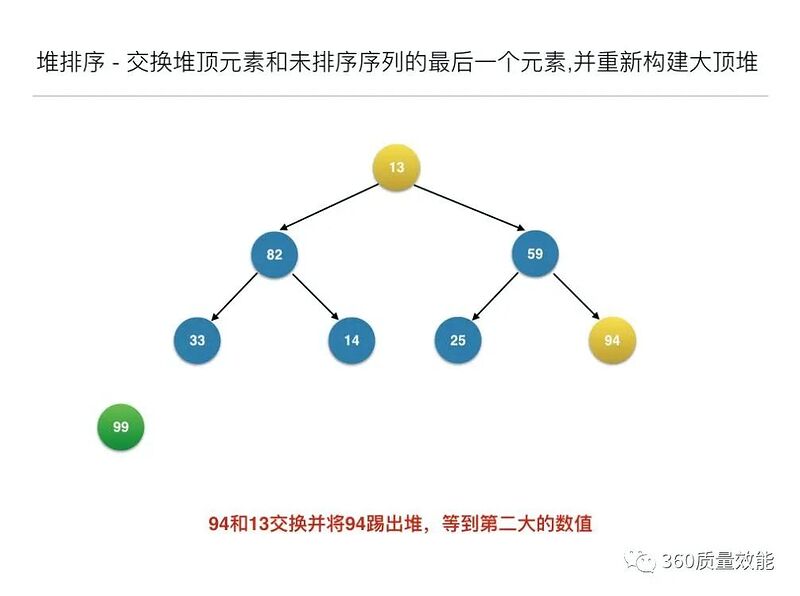
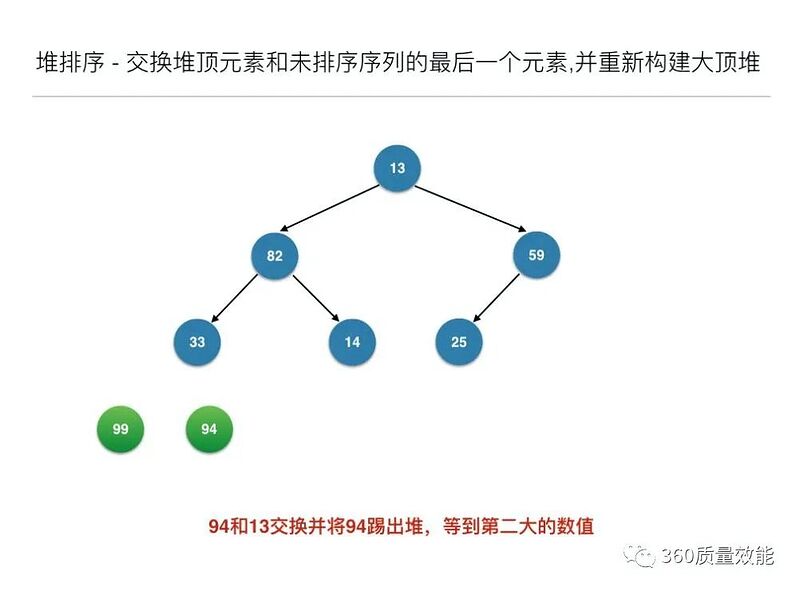
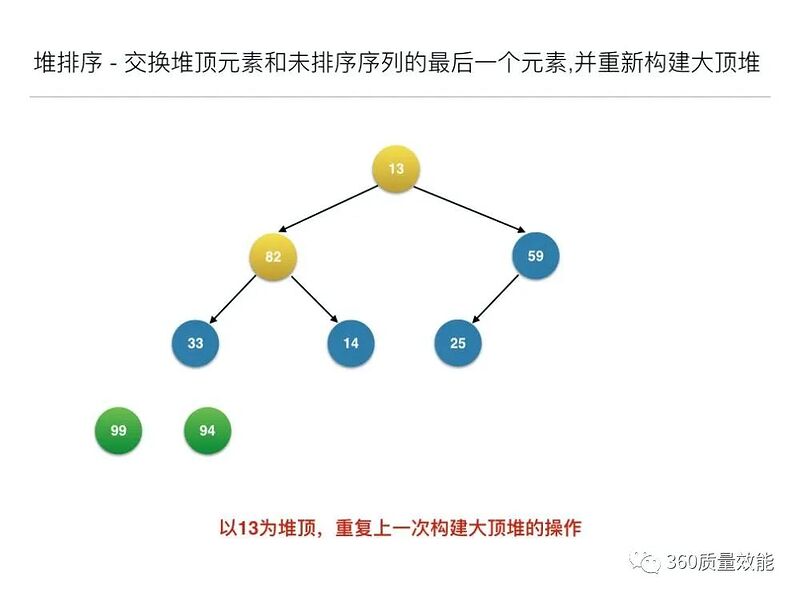
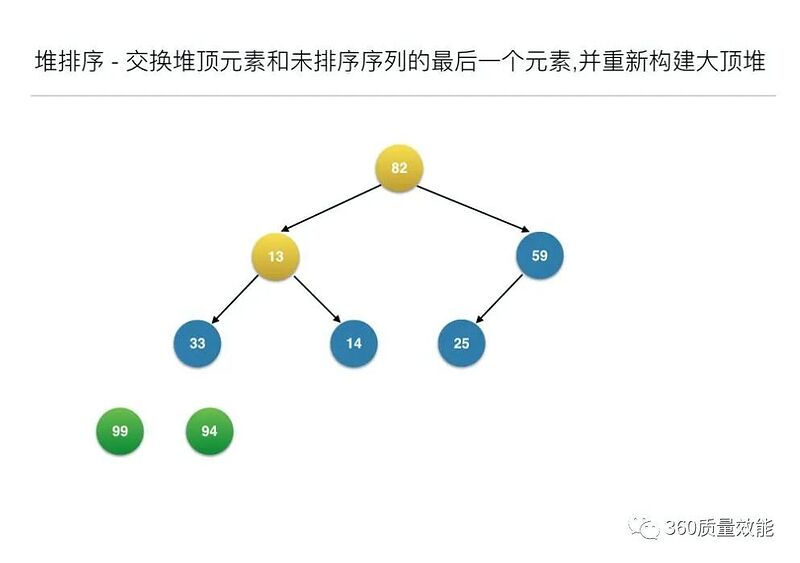
//交换堆顶元素和未排序序列的最后一个元素,并重新构建大顶堆
for (inti = len - 1; i> 0; i--) {
swap(arr, 0, i); // 元素交换
heapAdjust(arr, 0, i - 1);
}
}
/**
* 将arr[pos...off]构建成大顶堆
*
* @paramarr
* @parampos
* @param off
*/
public void heapAdjust(int[] arr, intpos, int off) {
int j, temp = arr[pos];
System.out.println("--此次循环的堆顶: " + temp);
intinit_j = pos * 2 + 1;
for (j = init_j; j <= off; j = j * 2 + 1) {
System.out.println("---循环索引值: " + j + " 数值: " + arr[j]);
if (j < off &&arr[j] <arr[j + 1]) {
System.out.println("---左右子节点对比: 左 " + arr[j] + " 小于右 " + arr[j + 1]);
++j;
}
// 节点不小于左右孩子节点
if (temp >= arr[j]) {
System.out.println("---此次循环的堆顶: " + temp + " 大于左右子节点!");
break;
}
int exchange = arr[j];
arr[pos] = arr[j];
pos = j;
arr[pos] = temp;
System.out.println("---交换位置: " + arr[pos] + " 和 " + exchange);
}
arr[pos] = temp;
System.out.println("--当前序列状态: " + Arrays.toString(arr) + "\n");
}
关键点
初始化大顶堆;
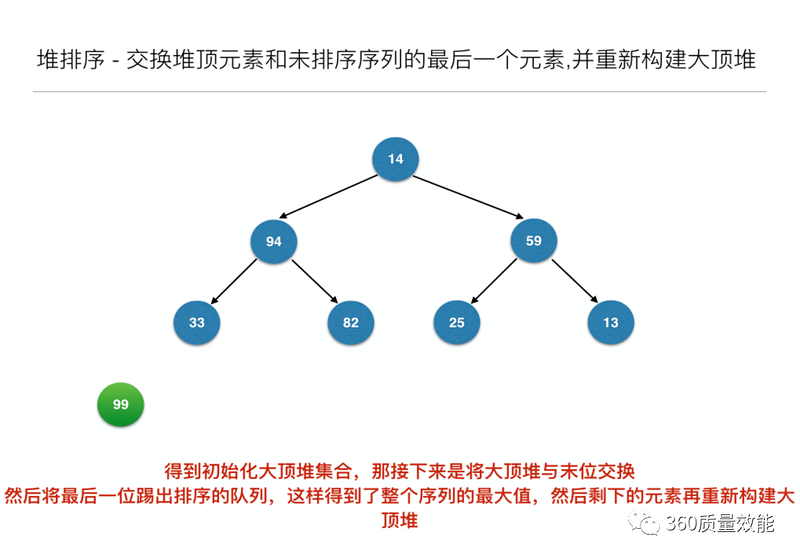
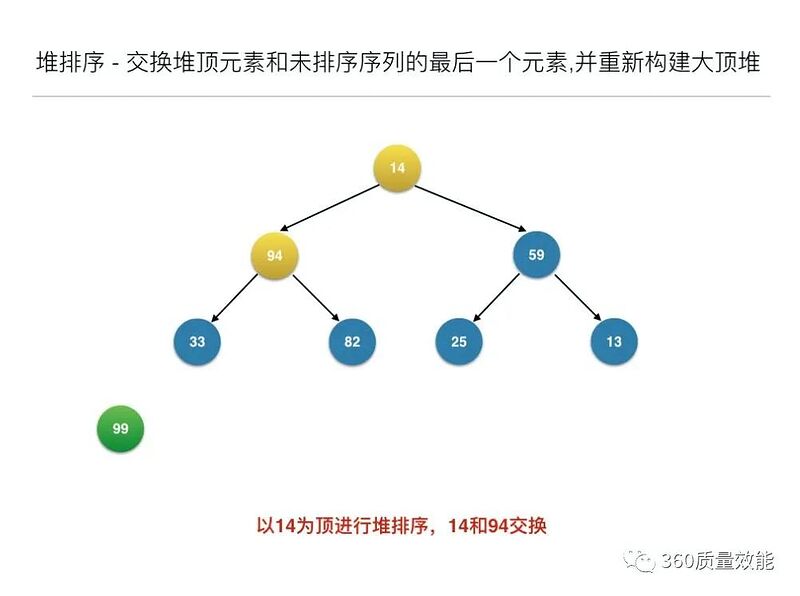
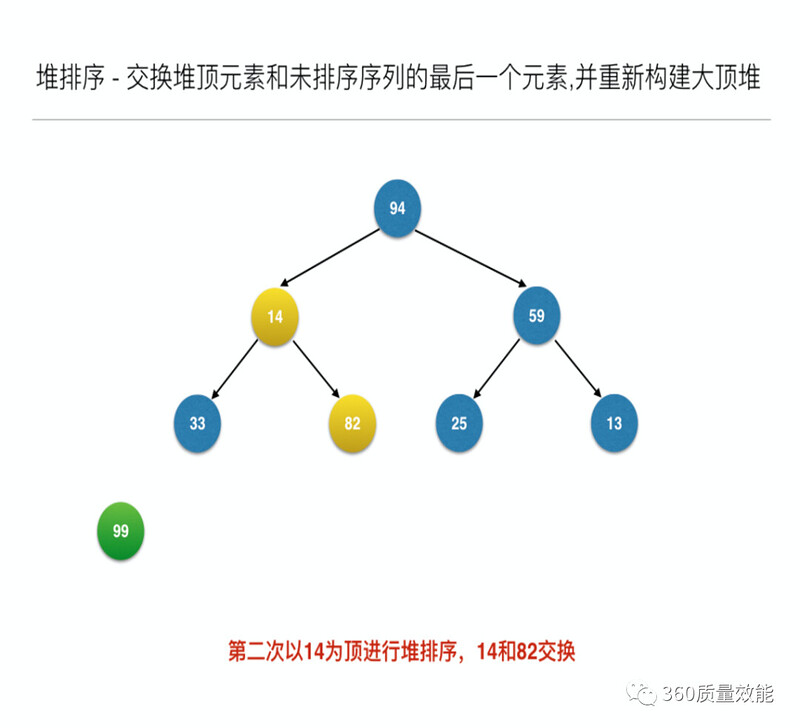
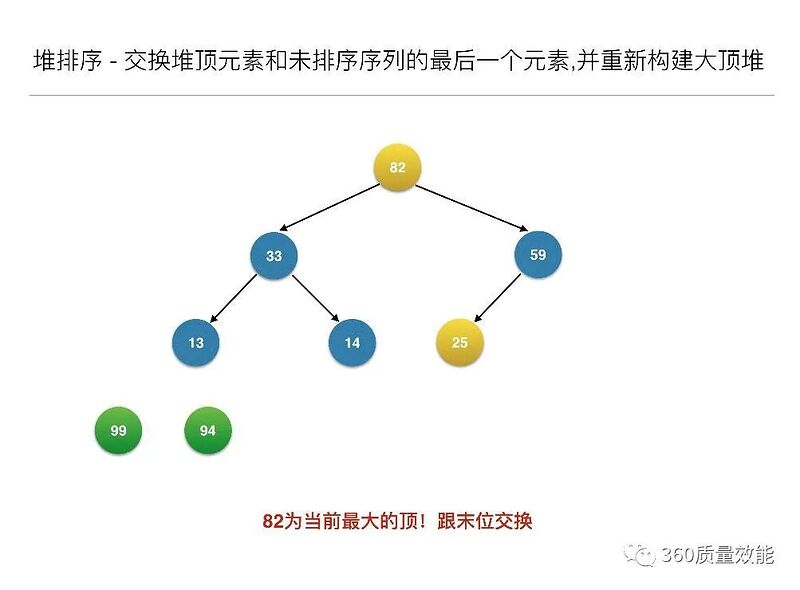
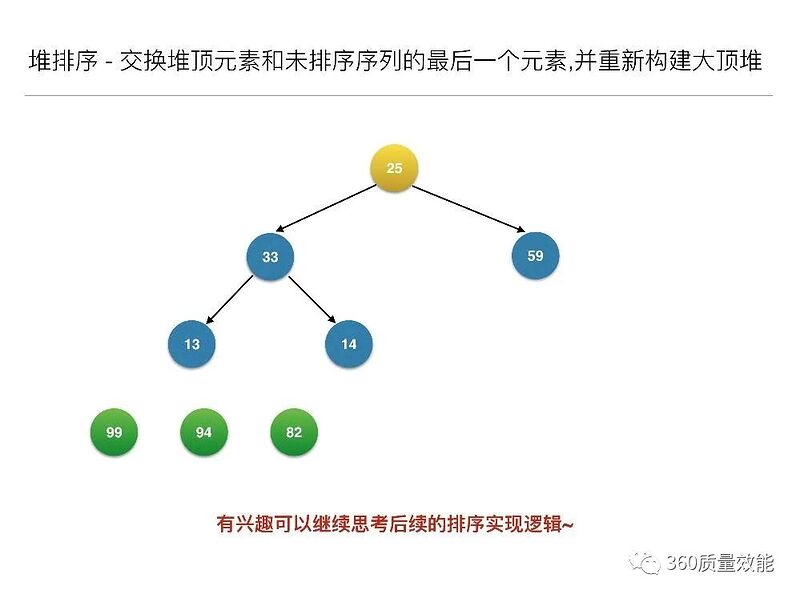
构建大顶堆之后,交换堆顶元素和未排序序列的最后一个元素,并重新构建大顶堆;
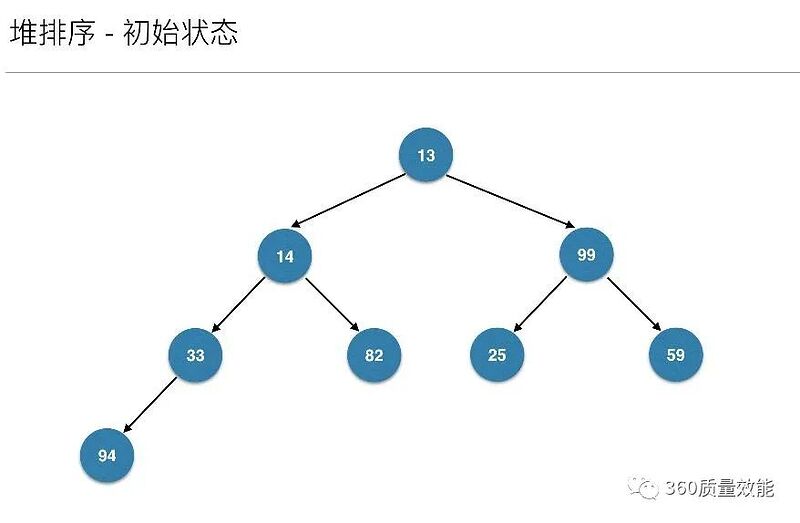
来了: 假设有一个初始集合 int arr = {13, 14, 99, 33, 82, 25, 59, 94};
那么len=arr.length=8,第一个for循环,代码第4行,i是从len/2-1=3开始,3→2→1→0的变量变化。
为什么不是从0到8,或者从8到0,而是从3到0呢?其实下图就很明白了。它们都是有孩子的结点。
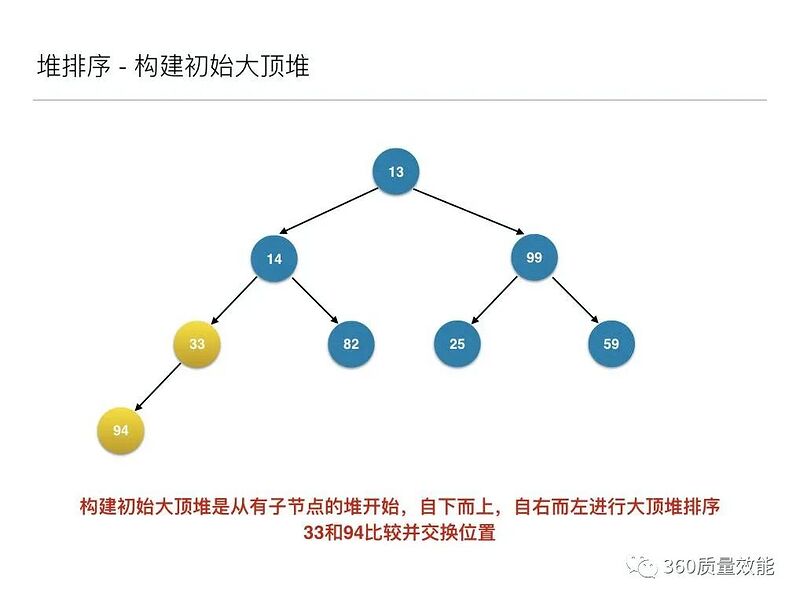
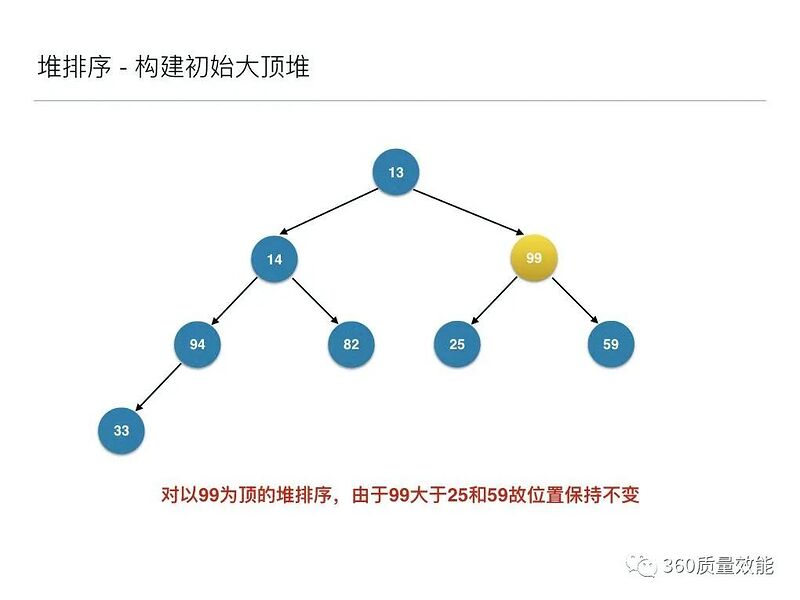
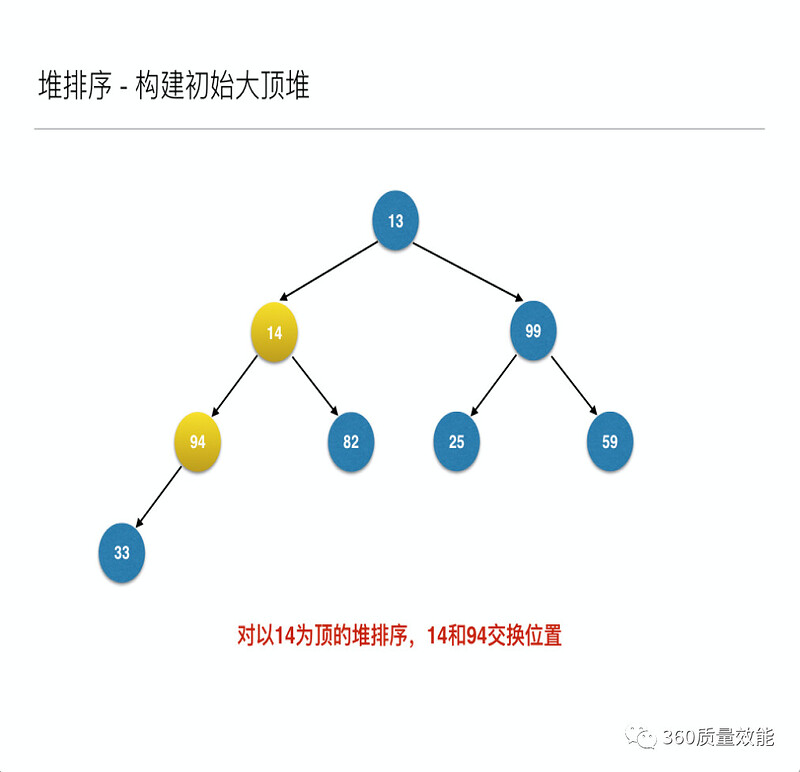
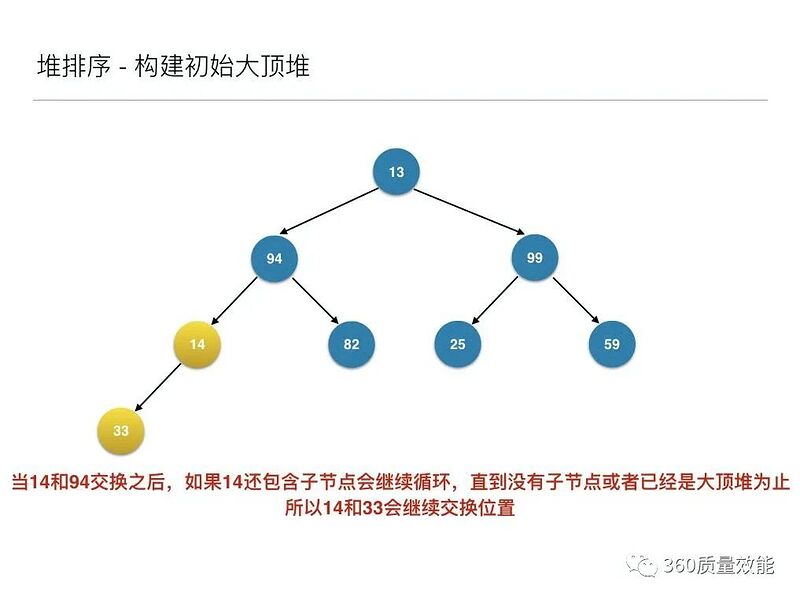
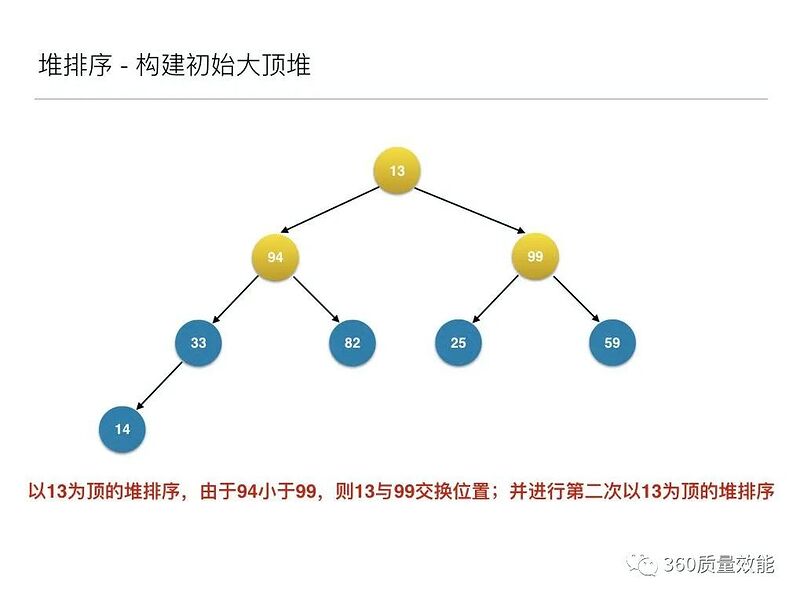
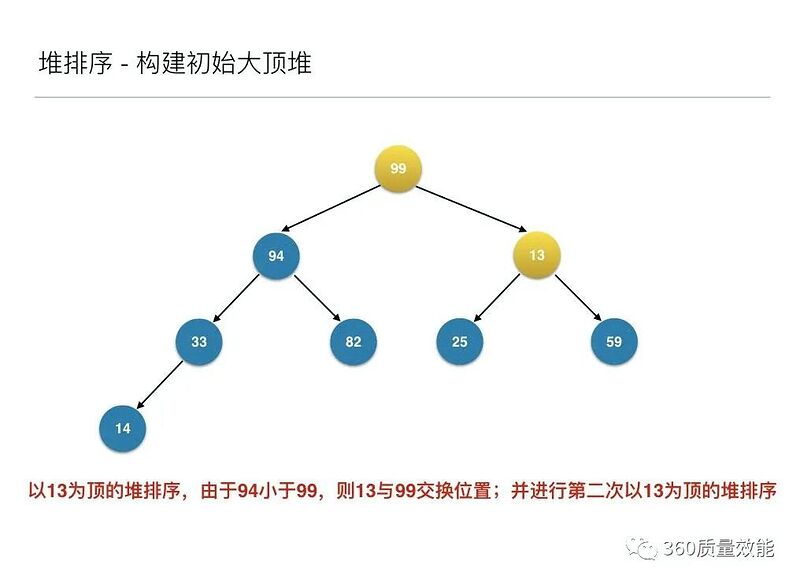
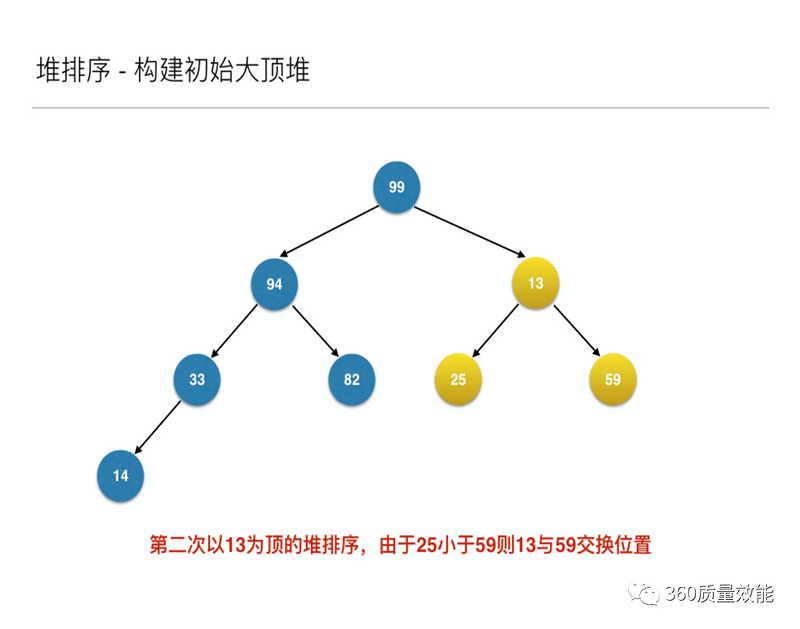
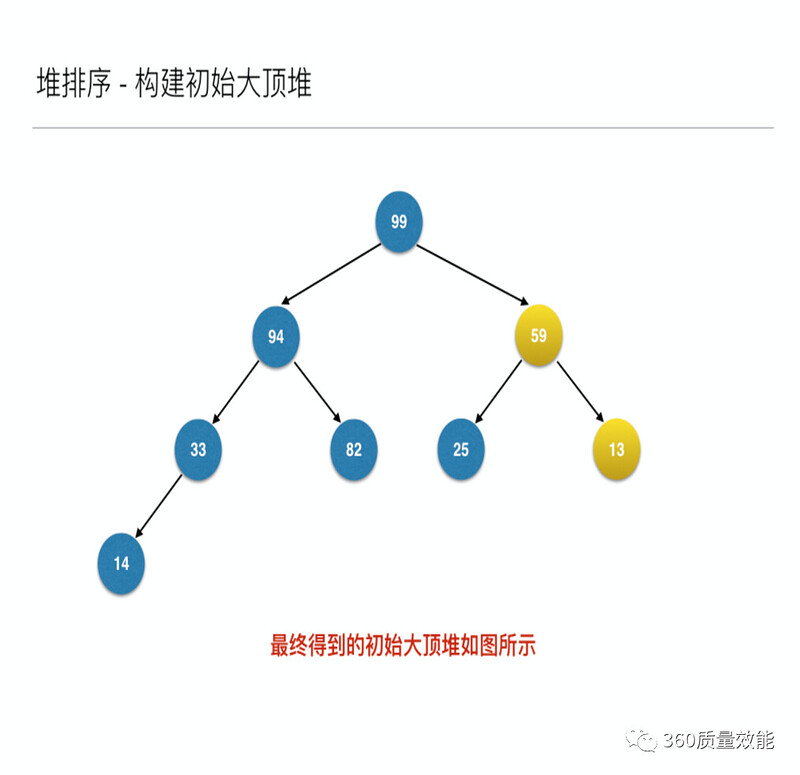
将待排序的序列构建成为一个大顶堆,其实就是从下往上,从右到左,将每个非终端结点(非叶结点)当作根结点,将其和其子树调整成大顶堆。
先构建成初始堆
到此为止构建大顶堆的过程算是完成了,任务完成了一半。接下来就是正式的排序过程,接着来
03
总结
首先由普通的数列联想到完全二叉树,然后利用完全二叉树的特性来实现记忆的功能,从而提高运行效率,只能由衷的佩服这个算法的提出者,太厉害了。
参考文献