To establish notation for future use, we’ll use x^{(i)}x (i)
to denote the “input” variables (living area in this example), also called input features, and y^{(i)}y (i)
to denote the “output” or target variable that we are trying to predict (price). A pair (x^{(i)} , y^{(i)} )(x (i) ,y (i) ) is called a training example, and the dataset that we’ll be using to learn—a list of m training examples (x(i),y(i));i=1,…,m—is called a training set. Note that the superscript “(i)” in the notation is simply an index into the training set, and has nothing to do with exponentiation. We will also use X to denote the space of input values, and Y to denote the space of output values. In this example, X = Y = ℝ.
To describe the supervised learning problem slightly more formally, our goal is, given a training set, to learn a function h : X → Y so that h(x) is a “good” predictor for the corresponding value of y. For historical reasons, this function h is called a hypothesis. Seen pictorially, the process is therefore like this:
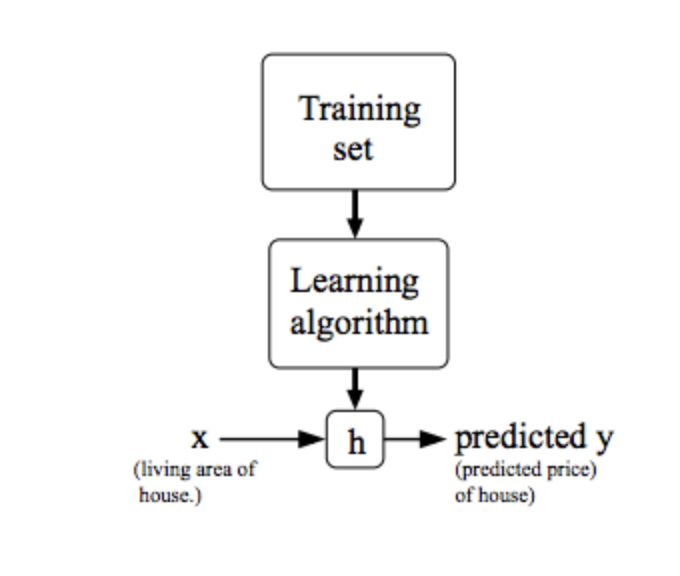
When the target variable that we’re trying to predict is continuous, such as in our housing example, we call the learning problem a regression problem. When y can take on only a small number of discrete values (such as if, given the living area, we wanted to predict if a dwelling is a house or an apartment, say), we call it a classification problem.
