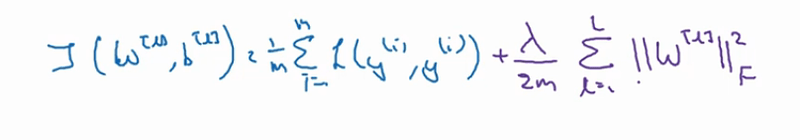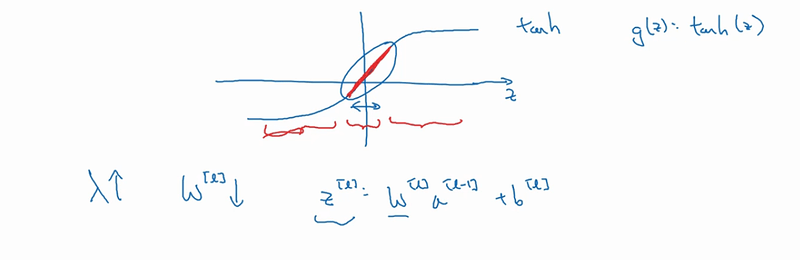测试集与训练集
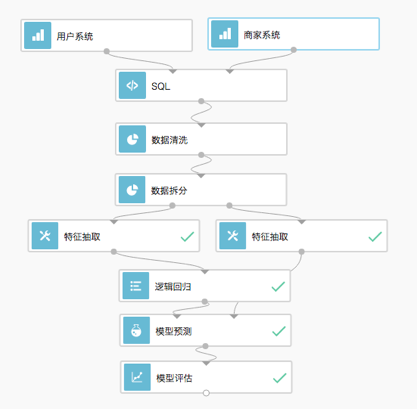
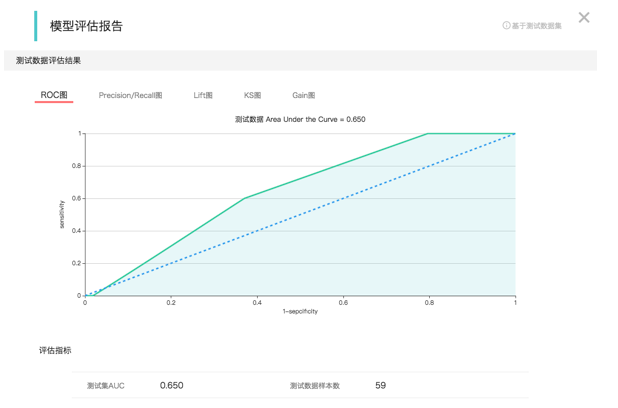
看上面的图,这是一个逻辑回归算法的 DAG(有向无环图),它是这个二分类算法的简单应用流程的展示。 可以看到我们在采集完数据并做过处理后,会把数据进行拆分。 训练集作用训练模型,而测试集会被输入到模型中来评估模型的性能。这是我们测试人工智能服务的最常用方式, 通过这个流程会产生一个模型的评估报告,如下:
当然这种拆分是有一定的规则的,如果数据集比较小,那么一般遵循 7:3 的经验拆分,7 分用来训练模型,3 分用来评估模型性能。 测试集不能太少,少了结果不准确,不能太多,太多了会导致训练集数据不足。 但这个规则不是死的。 如果数据集本身比较大,例如有 100W 行数据。那么我们抽取其中 1W 行做为测试集也就可以了。
偏差 (欠拟合) 和方差 (过拟合)
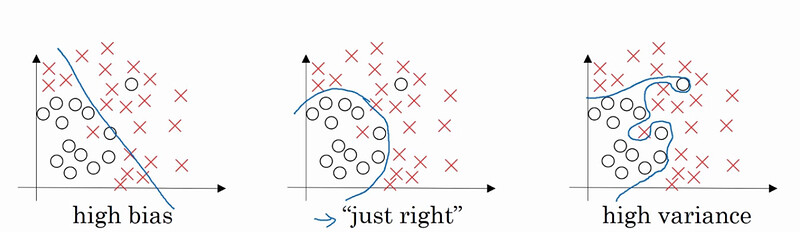
要解释这两个现象比较复杂,先从下面的图说起吧。
我们不论在逻辑回归,线性回归还是在神经网络中应用的都是线性函数。也就是我们一开始的公式:y=wx + b。 也就是我们上图最左边的图片中,是一条直线。分类算法比较直观一点的理解就是要在坐标空间中找到一个最适合的直线,让每个样本所在的点离这条线最近。但是直线的表达能力是有限的,就像上面最左边的图中一样,一条直线并不能很好的区分圆圈和叉叉,这时候我们会发现在训练集上训练的效果不好,也就是准确率不高,我们称这种情况为高偏差,也叫欠拟合。我们希望效果能像中间的图一样,是一条曲线,能够有效的增加正确率。 所以这时候激活函数出马了,我们在第一篇帖子中就写了激活函数其实并不是在激活什么,而是为我们的线性方程增加非线性效果。它为我们拟合了更好的效果。但有时候如果激活函数过度拟合就会产生上图中最后边的情况。 它拟合了一个非常复杂的线,这种情况的表现就是它的效果在训练集上非常好,误差很小。 但实际在测试集上表现的就很差。 例如我们在训练集上的误差 1%,而在测试集上额误差达到了 15%。 这是因为我们的线拟合的很复杂,很好的契合了训练集的数据分布,但是到了测试集的时候数据分布就不是这么回事了。那么如果出现了欠拟合或者过拟合该怎么办呢。 通常的做法如下:
对于欠拟合: 增加神经网络复杂度,出现欠拟合的原因之一是由于函数的非线性不足,所以用更复杂的网络模型进行训练来加深拟合。
对于过拟合:增加数据规模, 出现过拟合的原因之一是数据规模不足而造成的数据分布不均,扩展数据规模能比较好的解决这个问题。 当然另一个做法是正则化,下面我们将正则化
正则化 λ
有些时候扩展数据规模是很难的,所以我们采取使用正则化来解决过拟合问题,常用的是 L2 正则,其他的还有 L1 和 Dropout 正则。 这里主要说一下 L2 正则的原理,看下图:
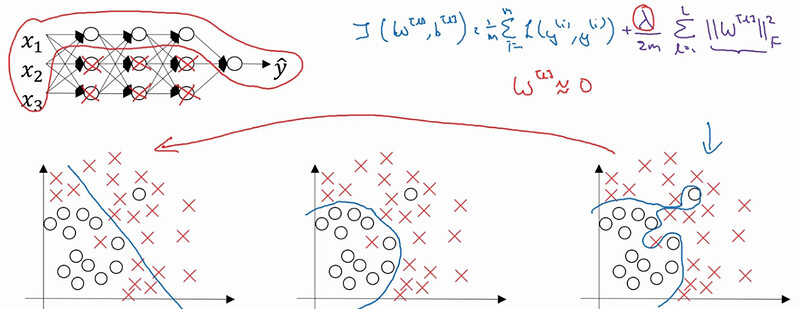
这是我们加了正则化之后的成本函数,可以看我们后面加入了正则化 λ 的表达式来完善成本函数。为什么加入λ能够减轻过拟合呢?直观一点的解释是设置的λ值越大,那么参数 w 的值就会被压缩的越小 (在梯度下降中, 每次迭代的步长,也就是这个公式 w=w - 学习率 * 成本函数对 w 的导数, 现在由于成本函数增加了正则项,使得 J 和 w 变得数值相关了)。 假设λ设置的足够大,那么 w 会无限的趋近于 0. 把多隐藏层的单元的权重设置为 0 以后,那么基本上就是消除掉了这些单元的作用,而使得网络模型得到简化,就像下面的图一样。由于正则化的设置,消除了一些隐藏单元的作用。而使得整个模型越来越接近于线性化,也就是从下图中的过拟合往欠拟合偏转。当然我们有一个适合的λ的值,能让我们的拟合状态达到最佳。 所以我们在训练模型的时候,往往都会有一个L2正则项的超参数需要我们设置。
更直观一点解释看下图:
这是我们的 tanh 激活函数, 可以看到当 z 的值越大时,整个函数的非线性就越大,而 z 的值越小 (图中红色加粗部分),函数就越是呈现出线性分布。 所以当我们增加λ的值, w 得值就越小,相应的 z 的值也就越小。因为 z = wx + b。 而我们第一次说激活函数的时候就说过神经网络中基本上是不使用线性函数作为激活函数的,因为不论有多少层,多少个单元,线性激活函数会使得所有单元所计算的都呈现线性状态。
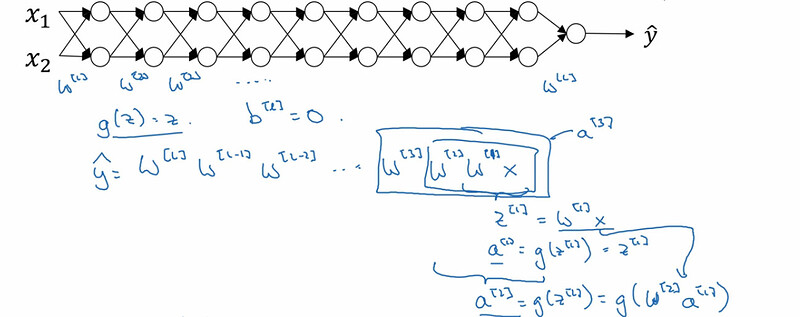
梯度消失与梯度爆炸
我们看上面的图,我们有一个很深的神经网络。 根据正向传播算法,我们看到 y的值是之前所有层的输入和权重相乘。这里我们先假设 g(激活函数) 是线性激活函数以方便我们理解,也就是说激活函数的作用消失了,因为是线性的,这个不多解释了。 在这里,假设我们让 w 初始化为 1.5。 我们会发现到最后 y的值会虽则层数的增多呈爆炸式增长,到最后我们计算成本函数 J 以及梯度下降中反向传播计算导数的时候也会发现呈爆炸式增长,这样的结果就是我们在梯度下降的过程中每一次迭代的步长非常大,这对我们找到最优解也就是最小值有非常大的阻碍,增加了我们的训练难度, 这就是梯度爆炸, 而如果我们让 w 的值为 0.5, y的值会随着层数的增多而呈现指数级的缩小,结果就是在梯度下降中每一轮迭代的步长非常小,导致于我们要用非常大的训练轮数去训练。 这十分影响训练的性能, 这就是梯度消失。 这就是为什么网络层数不能无限制的增长,因为这是给自己挖坑。 所以我们要做的就是合理化的初始化我们的 w 也就是初始权重。